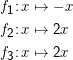
Die Mengen haben jeweils gleiche Kardinalität. Die Bijektionen sehen so aus:

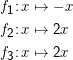
Es ist zugegebenermaßen etwas eigenartig, dass es genauso viele gerade Zahlen wie natürliche Zahlen gibt, denn immerhin wurde ja bei den geraden Zahlen jede zweite Zahl rausgelassen. Aber f₃ ist nun mal bijektiv. Hintergrund ist, dass “Unendlich” ein komischer Begriff ist, ℵ₀ eben keine richtige, sondern eine “transfinite” Zahl ist. Die Arithmetik auf diesen transfiniten Zahlen läuft etwas ungewöhnlich, man könnte mit gutem Recht sagen, dass ℵ₀ ∕2 = ℵ₀ ist.

Übrigens haben nicht alle unendlichen Mengen die Kardinalität ℵ₀ – die reellen Zahlen beispielsweise, die z.B. als beliebige (unendliche) Folgen von Ziffern zwischen 0 und 9 dargestellt werden können, haben eine höhere Kardinalität, es gibt keine Bijektion zwischen den natürlichen und den reellen Zahlen. Der Beweis dafür ist allerdings etwas aufwändig.