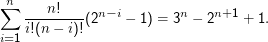
Grundgedanke ist, dass für den logischen Operator alles wahr ist, was überhaupt nur irgendein Bit gesetzt hat. Beim bitweisen Operator kommt nur dann etwas Wahres raus, wenn beide Operatoren an gemeinsamen Stellen Einsen haben. Wir können also z.B. 1 und 2 verunden und bekommen 0 (also falsch) heraus, während für den logischen Operator sowohl 1 als auch 2 wahr und sein Ergebnis also auch wahr ist.

Wie typisch ist das? Nun, zunächst ist diese Frage ziemlich irrelevant, solange wir einen Fall haben, in dem das Verhalten der logischen von dem der bitweisen Operatoren verschieden ist, müssen wir die beiden Operatoren sauber auseinanderhalten. Aber die Frage, bei wie vielen der möglichen Operanden das Problem auftaucht, ist trotzdem nützlich, schon, weil man damit ein Gefühl dafür bekommt, wie fies Fehler in dieser Kategorie in gutmütigen Fällen wohl sein werden.

Fangen wir mit 1-bittigen Operanden an. Es gibt 21 ⋅ 21 Kombinationen von Werten, von denen keine keine gemeinsamen gesetzten Bits haben, obwohl wie einzeln wahr sind. Nun, das ist nicht überraschend, für 1-bittige Operanden sind bitweise und logische Operatoren natürlich äquivalent.

Wie ist das bei 2-bittigen Operanden? Hier gibt es 22 ⋅ 22 Kombinationen. Dabei gibt es zwei Kombinationen, bei der die Operanden einzeln wahr sind, aber keine gemeinsamen Bits haben, nämlich (01,10) und (10,01). Das Problem taucht also bei 2∕24, mithin einem Achtel aller Werte auf.

3 Bit: Wir haben 23 ⋅ 23 Kombinationen. Einzeln wahr, aber ohne gemeinsame Bits sind (001,100), (001,010), (001,110), (010,001), (010,101), (100,011) sowie ihre Umkehrungen, also 12 Stück. Das Problem taucht also bei 10∕26 aller Werte auf – was etwas weniger als ein Sechsel ist. Immerhin taucht ist das Problem häufiger als bei n= 2, es scheint also mit wachsender Zahl der Bits mitzuwachsen. An dieser Stelle sollten wir wohl zum allgemeinen Fall übergehen.

n Bit: Zu einer n-bittigen Zahl z mit i gesetzten Bits gibt es 2(n-i) mögliche Zahlen z‘, die auf allen in z gesetzten Bits eine Null haben, denn i Stellen liegen fest, auf den restlichen n-i Stellen können noch je zwei Werte liegen. Eine dieser Zahlen z‘ ist allerdings die Null, und wir fordern ja, dass die z‘ C-wahr, also nicht-Null sind. Damit haben wir zu jedem z 2n-i - 1 Partner, für die das Problem auftaucht.

Wie viele n-bittige Zahlen mit i gesetzen Bits gibt es? Man kann das elementar herleiten, aber es ist bequemer, ein Urnenmodell heranzuziehen (in diesem Fall: Ziehen der i Positionen der gesetzten Bits aus n Möglichkeiten ohne Zurücklegen, wobei die Anordnung keine Rolle spielt). In der Stochastik lernt man, dass es nach dieser Überlegung n!∕i!(n-i)! mögliche Zahlen gibt (das Ausrufezeichen steht für die Fakultät). You weren’t supposed to know this.

Demnach gibt es zu jeder Zahl i von gesetzten Bits n!∕i!(n-i)!(2n-i - 1) “schlechte” Fälle. Wir müssen die Beiträge von i= 1,2,3,…,n zusammenaddieren (warum nicht i= 0?) und kommen so auf den Ausdruck

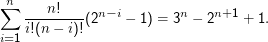
∑n i!(nn!--i)!(2n - i - 1) = 3n - 2n+1 + 1. i=1

Die Berechnung der Summe ist nicht ganz trivial, ich selbst habe mich über das Gleichheitszeichen mit einem Computeralgebrasystem gemogelt. Jedenfalls: Die Formel stimmt, was ihr, wenn ihr wollt, mit dem folgenden Programm nachprüfen könnt:

#include <stdio.h>

#define MAX (1<<5)

int main(void)
{
  unsigned int i, j;
  unsigned int count=0;

  for (i=1; i; i=(i+1)%MAX) {
    for (j=1; j; j=(j+1)%MAX) {
      if (!!(i&j) != (i&&j)) {
        count++;
      }
    }
  }
  printf("%d\n", count);
  return 0;
}

– tragt bei MAX das n ein und vergleicht (für kleine n, dieser “Algorithmus” hat quadratische Laufzeit). Macht euch klar, warum dieses Programm alle “schlechten” Fälle findet.

Nun gibt es 22n Paare von n-bittigen Zahlen. Der Anteil der “schlechten” Fälle ist also (3n - 2n+1 + 1)∕22n. Steigt er mit n oder nicht? Nun, um die Asymptotik zu finden, wandeln wir erst alles auf eine Basis und dividieren durch den am stärksten wachsenden Term:

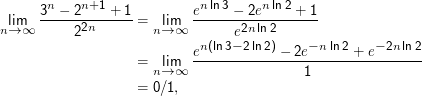
3n---2n+1-+--1- en-ln-3---2en-ln2-+-1- nli→m∞ 22n = n→lim∞ e2nln2 n (ln3- 2ln2) - nln2 - 2n ln 2 = lim e---------------2e-------+-e-------- n→ ∞ 1 = 0∕1,

wobei der erste Term im Nenner gegen Null geht, weil ln3 < 2ln2. Mit anderen Worten geht der Anteil “schlechter” Fälle für große n gegen Null, der Eindruck, er steige mit n, den wir bei n= 3 hatten, war nur ein Artefakt der kleinen Zahl (Lehre: Vorsicht mit “unvollständiger Induktion”).

Nochmal: You weren’t supposed to know all this.

Beim Odern gibts diesen Typ von Problem nicht. Wenn auch nur ein Bit in einem der Operanden gesetzt ist, ist sowohl a|b als auch a||b wahr, im anderen Fall sind beide falsch. Hier bleibt allerdings noch das Problem, dass | nicht kurzschließt, d.h. immer alle Operanden auswertet – und auch das kann böse Fehler verursachen.