Es ist 103∕210 = 0.976, dem kB fehlen also ungefähr 2.5% zum kiB.

Weiter ist 106∕220 = 0.953, dem MB fehlen also ungefähr 5% zum MiB.

Schließlich ist 109∕230 = 0.931, dem GB fehlen also ungefähr 7% zum GiB.

Bei der Asymptotik müssten wir zunächst klären, wie wir wir dezimale und binäre Präfixe identifizieren wollen – wollen wir zu jeder Zehnerpotenz jeweils die wertmäßig nächste Zweierpotenz nehmen? In dem Moment wäre die Frage nach der Asymptotik reichlich sinnlos, weil wir sie schon auf irgendwas in der Gegend von eins erzwungen haben.

Also fragen wir nach dem Limit von 10n∕210n∕3 – das ist der allgemeine Ausdruck für das, was wir oben berechnet haben. Wir verwenden wieder yx = ex ln y und ziehen die Exponentialfunktion zusammen, was auf exp(n(ln10 - 10 3 ln2)). Nun geht exp(an) für a < 0 gegen Null, für a > 0 gegen Unendlich (was ist mit a= 0?) Wenn man ln10 - 10 3 ln2 ausrechnet kommt man auf -0.0079…, d.h. das Verhältnis geht gegen Null.

Mit anderen Worten wird das Problem der Unterschiede zwischen dezimalen und binären Präfixen mit wachsenden Datenträgergrößen immer dramatischer. Bei welchem n ist dezimal nur noch halb so viel wie binär? Nun:

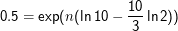
10 0.5 = exp (n (ln 10 - ---ln2)) 3

lässt sich durch Logarithmieren auf beiden Seiten zu

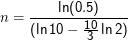
ln(0.5) n = --------10------ (ln 10 - 3 ln 2)

auflösen. Ausgerechnet führt das auf ungefähr 88. 1088 ist weit jenseits aller für Speicher und ähnliches interessanten Zahlen – die komplette Erde hat so gegen 1050 Atome, man bräuchte also gegen 1038 Erden, um so viele Daten zu speichern, selbst wenn man in jedes Atom ein Byte speichert.

Eine ähnliche Rechnung für die Frage, wann man 10% Unterschied hat, liefert gut 13. 1013 Bytes sind 10 Gigabytes, also eine kleine Festplatte. Wenn man Kapazitäten in GiB statt in GB angibt, würde aus einer 10GB-Platte also plötzlich eine 9GiB-Platte. Das mag schon ein kommerzieller Nachteil sein.