Formale Sprachen sind Mengen von Wörtern (in linguistischen Anwendungen können das “Wörter”, Sätzen, Phrasen oder was immer sein, in Anwendungen aus der Informatik vielleicht eine ganze Datei), die ihrerseits aus Symbolen (diese können je nach Anwendung Buchstaben, “Wörter” einer Natursprache oder allgemeiner “Tokens”, vorklassifizierte Bruchstücke einer Eingabe aus einer vorgeschalteten lexikalischen Analyse) aufgebaut sind. Was in der Menge ist, ist ein “grammatisch korrektes” Wort, alles andere ist falsch.
In dieser Veranstaltung werden wir die Symbole meist klein halten: a, b, oder y (die Methoden funktionieren aber genauso mit Symbolen wie “der”, “Mann”, “Xylophon”, “Magnetostriktionskoeffizient” oder auch +, - und ×), dementsprechend sehen die Wörter meist albern aus: abyby.
Chomsky hat in den 50er und 60er Jahren angefangen, Natursprachen als formale Sprachen zu behandeln. Es ist zu bezweifeln, dass das ganze Geheimnis ist, formale Syntaxanalyse aber wird bei der Verarbeitung natürlicher Sprache immer irgendwo auftauchen. Kunstsprachen (Programmier- oder Konfigurationssprachen, Protokolle) basieren fast vollständig auf Theorien formaler Sprachen.
Wir wollen einem Rechner erklären, wie er eine Sprache “verstehen” kann, und Abschätzungen gewinnen, wie schwierig das sein wird. Dabei werden wir nach “guten” Sprachen suchen, in denen eine Entscheidung über die “Richtigkeit” (“Grammatikalität”) eines Wortes “leicht” gefällt werden kann.
Näher an die Natursprache rücken: Seien Zeichen in etwa das, was im Duden als Wörter steht (plus Flexionen), Wörter in etwa das, was zwischen zwei Satzendepunkten steht. Dann kann man Wörter beispielsweise in ihre Phrasenstruktur zerlegen und als Baum darstellen:
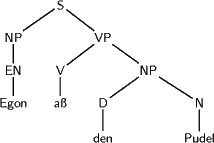
Eine Grammatik soll aus Klauseln wie
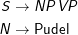
Bevor wir uns aber wirklich mit Sprachen, Regeln, Bäumen und ähnlichem beschäftigen können, müssen wir zunächst einige mathematische Grundlagen schaffen. Das Ziel dabei ist, dass wir “zwingend” argumentieren können wollen, d.h. unsere Begriffe sollen unzweideutig sein, und wenn wir etwas beweisen, muss dieser Beweis von allen, die die Grundlagen der Mathematik anerkennen (für uns heißen diese Grundlagen übrigens “Axiomensystem von Zermelo und Fränkl” – aber so weit “runter” wollen wir in diesem Rahmen nicht gehen) überprüfbar sein.
Für dieses Ziel gibt es zwei Gründe. Einerseits ist es eine Frage der Erkenntnistheorie – wir wollen vermeiden, dass sich Leute etwa endlos streiten, was nun ein Wort sei (und so ein Streit ist im Rahmen natürlicher Sprachen erstaunlich schwer zu entscheiden). Andererseits soll unser Vorgehen so zwingend sein, dass sich ihm nicht mal ein Computer entziehen kann (und nicht mal ein Computer der auf dem Mars gebaut wurde). Das bedeutet, dass die Erkenntnisse, die wir in diesem Rahmen gewinnen, mehr oder minder direkt in Computerprogramme übersetzbar sind. Sowas hilft ungemein, wenn man Computerlinguistik treiben möchte…