In der Mathematik gibt es viel zu bezeichnen, und weil das, was bezeichnet wird, noch viel manipuliert werden soll, sollten die Zeichen kurz sein. Deshalb braucht man viele Zeichen. Im Laufe der Geschichte der Mathematik haben sich etliche Konventionen herausgebildet, mit denen man vertraut sein sollte.
Insbesondere solltet ihr die Namen und Sprechweisen kennen. Wenn ihr irgendwelche mathematischen Ausdrücke hinschreibt, prüft dann und wann, ob ihr sie auch “aussprechen” könnt – wenn nicht, seht hier nach, wie man das spricht oder fragt in der Vorlesung oder im Tutorium. Am Ende müsst ihr etwa in Prüfungen oder gegenüber Mitstudis und KollegInnen, ja doch immer wieder über Mathematik reden.

Fast alle Zeichen in der Mathematik sind mehrfach überladen, bedeuten also je nach Kontext verschiedene Dinge. Es gibt also keine Tabelle, die sagt “Σ ist ein Alphabet, während ν eine Frequenz ist.”
Sprechweisen: f‘: “f Strich” (engl. f prime); 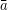 : “a quer” (engl. a bar); â: “a Dach” (engl. a hat); ai: ahh ihh.
: “a quer” (engl. a bar); â: “a Dach” (engl. a hat); ai: ahh ihh.
Ein paar Zeichen haben kanonische Bedeutungen. Hier eine Auswahl, ohne Gewähr, dass sie diese im konkreten Fall auch haben:
- ∞– unendlich (schwieriger Begriff)
- i – imaginäre Einheit. Leider ist i auch der populärste Index, also eine Variable, die einfach nacheinander verschiedene Werte annimmt (es geht dann meist weiter mit j, k usf.) Hier wird also eifrig überladen. Da wir hier nicht mit komplexen Zahlen operieren, bedeutet i hier auch fast nie die imaginäre Einheit, und wenn, ist das Zeichen nicht kursiv, was es als Index immer ist.
- ∅ oder {}– die leere Menge (engl. empty set)
- ∑ – Summe
- ∏ – Produkt
- ∈– Mitgliedschaft von Mengen (Sprechweise: a∈B– “a Element B” oder “a ist in B”, engl. “a is an element of B” oder “a in B”)
- ∪– Vereinigung von Mengen (Sprechweise: A∪B– “A vereinigt B”, engl. “A union B”)
- ∩– Schnitt von Mengen (Sprechweise: A∩B– “A geschnitten B”, engl. “A intersection B”)
- \– Differenz von Mengen
- ×– kartesisches Produkt von Mengen (Sprechweise: A kreuz B)
- ∘– “Verkettung von Funktionen” oder “generischer Operator”
- ≈– Ungefähr gleich
- ~– Ungefähr gleich oder Proportional
- ≫, ≪– Wesentlich größer, kleiner
- →– “Geht über auf” (engl. “maps to”)
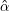 ∈Γ
∈Γ