(1)
Malt die Wahrheitstafeln für 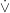 (Exklusiv-Oder, also Entweder-Oder), ∧ und ¬.
(Exklusiv-Oder, also Entweder-Oder), ∧ und ¬.
Aussagen sind Dinge, die wahr oder falsch sein können: “a ist im Wort Markus enthalten” (W), “Alle Vögel fliegen hoch” (F).
2 + x= 7 ist keine Aussage, solange x nicht belegt ist: Aussageform.
Junktoren sind Operatoren auf Aussagen: Sie bauen aus Aussagen neue Aussagen:
Beispiele: Wenn ¬A wahr ist, ist A falsch Wenn A1 wahr und A2 falsch ist, ist A1 ∨A2 wahr und A1 ∧A2 falsch.
Die Wirkungsweise der logischen Operatoren wird gerne durch Wahrheitstafeln dargestellt, hier für Disjunktion, Implikation und Äquivalenz.
| A1 | A2 | ∨ | → | ↔ | |
| W | W | W | W | W | |
| W | F | W | F | F | |
| F | W | W | W | F | |
| F | F | F | W | W |
Es mag zunächst etwas verwirren, dass etwas wie “folgt aus” hier den intuitiv verstehbaren logischen Operatoren “und” und “oder” gleichgestellt sind. Das Problem dahinter ist, dass man unterscheiden sollte zwischen dem Erzeugen neuer Aussagen und den Aussagen selbst. Das “folgt aus”, das ihr in der Schule wahrscheinlich mit ⇒ und (bzw. ⇔ für “ist äquivalent mit”) bezeichnet habt, gehört zur ersten Kategorie – es macht eine Aussage über die Relation zwischen (anderen) Aussagen, gehört also in gewisser Weise zu einer Metasprache. Da die Trennung dieser Ebenen im harten Beweisleben meist nicht dringend nötig ist, wird sie auch oft nicht vorgenommen, und auch wir werden nach dieser Seite für unsere Schlüsse einfach ⇒ schreiben.
Das ←, das hier gemeint ist, sollte man sich vorstellen wie in Aussagen der Form “Wer mehr als 50% der Punkte erreicht, wird zur Scheinprüfung zugelassen” oder “Wenn der Computer läuft, wird er kalt”. Beide haben die Form A→B (macht euch klar, was jeweils A und B sind!), aber die eine ist für diese Veranstaltung wahr, die andere für unsere Computer falsch (das mit dem “für XY” ist übrigens etwas, mit dem die Logik auch eifrig operiert, das Stichwort hier wären Belegungen).
Komisch an der Tabelle ist vor allem, dass F→X wahr, egal ob X selbst wahr oder falsch ist. In der Tat ist das nicht wirklich trivial (das Stichwort dazu ist “ex falso quodlibet”), und eine stichhaltige Begründung (sofern es so etwas an den Grundlagen geben kann) baut letztlich auf Kalküle auf, mit denen man Aussagen generiert. Es ist aber vielleicht einsichtig, dass etwas wie “Wenn die Sonne im Westen aufgeht, ist es 12 Uhr mittags” eigentlich nicht falsch sein kann.Die Sonne geht eben nie im Westen auf, und deshalb ist es egal, ob es gerade 12 Uhr mittags ist, wenn sie das tut. In dem Sinn kann die Aussage jedenfalls nicht falsch sein. Wenn die Aussage aber nicht falsch ist, muss sie in der klassischen Logik (in der es nichts außer wahr und falsch gibt) aber wahr sein (ok, das war jetzt ein Taschenspielertrick – wie gesagt, letzlich kann man das akzeptieren oder nicht und kommt entsprechend auf verschiedene Logiken, und wer klassische Logik machen will, sollte es akzeptieren).
Die Äquivalenz (“dann und nur dann”) wird auch gerne mit “gdw” (“genau dann wenn”) oder “iff” (“if and only if”) abgekürzt.
Häufig reichen einfache Aussagen nicht aus – man will Aussageformen mit Variablen belegen können, und dann soll wieder etwas herauskommen, was wahr oder falsch ist. Dazu gibt es Quantoren:
Beispiel: ∀a∈ℕ ∃b∈ℤ : b= a- 1 heißt: Für alle a aus der Menge ℕ gibt es ein b in der Menge ℤ, so dass die Gleichung b= a- 1 gilt
Die Quantoren kommen aus einer Sprache, die sich Prädikatenlogik nennt und zusätzlich noch genau sagt, was eigentlich alles hinter den Quantoren kommen kann. Für unsere Zwecke sind diese Details nicht sonderlich wichtig, ich möchte nur darauf hinweisen, dass richtige Logiker mit Schreibweisen wie “∀x∈ℕ” nicht unbedingt immer glücklich sind, weil man damit leicht den Rahmen dessen, was in dem Formalismus der Prädikatenlogik erster Stufe erlaubt ist, verlassen kann. Nicht erlaubt wäre beispielsweise ∀A∈{A|A ist für natürliche Zahlen wahr}. Warum das so ist, soll uns hier nicht kümmern, mein Punkt ist, dass sind diese Zeichen eigentlich mehr als die Abkürzungen, als die wir sie hier verwenden.
Das ist in der Mathematik generell so: Die lustigen Zeichen, die hier verwendet werden, dienen nicht nur dazu, Leute zu beeindrucken, sie vermitteln auch eine präzise und tragfähige Semantik, die im Prinzip jedem/r ermöglicht, die Argumentationsweisen unzweideutig nachzuvollziehen und eventuelle Widersprüche aufzudecken. Ein leicht nachvollziehbares Beispiel dazu findet sich in den Aufgaben: Der Satz “Es regnet oder ich fahre Rad” hat in Natursprache mindestens zwei mögliche Interpretationen (“Inklusiv-oder” oder “Exklusiv-oder”, wobei ersteres erlaubt, dass beides wahr ist, letzteres aber dem Entweder-oder entspricht) – die formalisierte Aussage hat genau eine, nämlich die Inklusiv-Variante.
Mehr zu all diesen Themen vermittelt die Vorlesung über Logik.
Ihr solltet euch wenigstens an den rötlich unterlegten Aufgaben versuchen
(1)
Malt die Wahrheitstafeln für 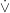 (Exklusiv-Oder, also Entweder-Oder), ∧ und ¬.
(Exklusiv-Oder, also Entweder-Oder), ∧ und ¬.
(2)
(a) Sei R die Aussage “es regnet”, F die Aussage “ich fahre Rad” und N “ich werde nass”. Schreibt die folgenden Aussagen als formale Ausdrücke:
(b) Bewertet den Wahrheitsgehalt der folgenden Aussagen zum augenblicklichen Zeitpunkt:
(3)
Berechnet Wahrheitstafeln für die Aussagen A∨ (B∧C) und (A∨B) ∧ (A∨C). Da hier drei Wahrheitswerte eine Rolle spielen, haben diese Wahrheitstafeln 23 = 8 Zeilen, eben alle Möglichkeiten, A, B und C zu belegen.