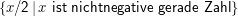Naiver Mengenbegriff
Georg Cantor (1895): Eine Menge M ist eine Zusammenfassung von bestimmten wohlunterschiedenen Objekten unserer Anschauung oder unseres Denkens, welche Elemente der Menge M genannt werden, zu einem Ganzen.
Wichtige Folge dieser Definition: Mengen sind nicht geordnet ({a,b}= {b,a}), ein Element kann nicht “mehrmals” Element einer Menge sein.
Die Definition ist weniger trivial, als sie klingen mag. Sie impliziert inbesondere bereits das unten erwähnte Extensionalitätsprinzip. Sie bedeutet aber wohl oder übel auch, dass Mengen als Elemente von Mengen in Frage kommen (was etwas ganz anderes ist als eine Teilmenge). Das ist zwar sehr nützlich (genau genommen entscheidend), kann aber, wenn man unvorsichtig ist, Probleme machen:
Russell’sche Antinomie
Sei M die Menge aller Mengen, die sich nicht selbst enthalten. Wenn M∈M, dann folgt nach Definition, dass M∉M. Wenn M∉M, folgt nach Definition, dass M∈M.
Also: Naiver Mengenbegriff führt zu Widersprüchen, offenbar sind zusätzliche Forderungen nötig: Axiomatische Mengenlehre, ZFC.
Für unsere Zwecke reicht der naive Mengenbegriff allerdings, wo er Probleme bereiten würde, weise ggf. darauf hin. Die Axiomatische Mengenlehre ist nämlich, richtig betrieben, Stoff für mehr als eine eigene Vorlesung.
Übrigens ist die Russell’sche Antinomie eng verwandt mit Aussagen wie “Alle Hochschullehrer lügen”, wenn ich ihn sage: Es nutzt ein Selbstanwendungsproblem aus, ein Formalismus (im einen Fall die Mengenlehre, im anderen die Sprache) wird auf sich selbst angewandt. Ein solches Selbstanwendungsproblem wird uns bei der Untersuchung von Turingmaschinen und ihren Beschränkungen noch einmal begegnen.
Mengen notieren wir entweder durch Aufzählung ihrer Elemente,
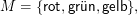
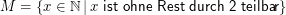
oder durch Basis und Regeln rekursiv, z.B.:
- a∈A
- Φ ∈A⇒Φa∈A
- Elemente von A sind nur Zeichenketten, die durchdie obigen Regeln erzeugt wurden (diese Ausschlussbedingung werden wir künfig implizit annehmen)
erzeugt A= {a,aa,aaa,aaaa,…}.