6. Mengen II

Teilmengen

B ist Teilmenge von A (B⊆A), wenn

$x ∈ B ⇒ x ∈ A$

gilt. Also: Jedes Element von B ist in A enthalten.B ist echte Teilmenge von (oder echt enthalten in) A (B⊂A), wenn

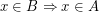
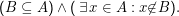
$(B ⊆ A ) ∧ ( ∃x ∈ A : x<ignored>⁄∈< /ignored>∉B ).$

Das heißt: B ist Teilmenge von A, und dazu existiert mindestens ein x∈A, das nicht in B ist.

Vorsicht: B∈A ist etwas ganz anderes als B⊂A.

Extensionalitätsprinzip

Zwei Mengen sind gleich, wenn sie die gleichen Elemente haben: A= B⇔B⊆A∧A⊆B.

Leere Menge

Eine Menge ohne Element ist wegen Extensionalität immer gleich der Leeren Menge

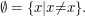
$∅ = {x|x<ignored>⁄=< /ignored>≠x}.$

Es gilt: ∅⊆M für alle Mengen M.

Der Beweis dazu ist eine nette Illustration von Schlussweisen in der Mathematik:

Die zu zeigende Aussage lässt sich als x∈∅⇒x∈M schreiben – hier wurde einfach die Definition der Teilmenge verwendet.

Dies ist äquivalent zu x≠x⇒x∈M. Ist diese Aussage wahr oder falsch? Nun, x≠x ist immer falsch, d.h. auf der linken Seite der Aussage steht F. Eine Inspektion der Wahrheitstafel von ⇒ liefert, dass damit unabhängig von vom Wahrheitswert der rechten Seite die Gesamtaussage immer wahr ist. Da alle unsere Aussagen äquivalent sind, ist auch die zu beweisende Ursprungssaussage wahr.

Auf ähnliche Weise können viele Eigenschaften der leeren Menge nachgewiesen werden – offenbar spielt die leere Menge in der Mengenlehre eine ähnlich exotische Rolle wie die Null in der Arithmetik.

Operationen auf Mengen

Vereinigung:

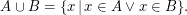
$A ∪ B = {x |x ∈ A ∨ x ∈ B }.$

Schnitt:

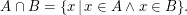
$A ∩ B = {x |x ∈ A ∧ x ∈ B }.$

Differenz:

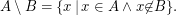
$A \ B = {x |x ∈ A ∧ x< ignored>⁄∈</ignored>∉B }.$

Komplementbildung (relativ zu Obermenge O):

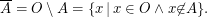
$-- A = O \ A = {x|x ∈ O ∧ x<ignored>⁄∈< /ignored>∉A}.$

Bei der Komplementbildung ist entscheidend, dass wir eine Obermenge haben. Hätten wir sie nicht, wäre im Komplement “alles”, was nicht in der Menge ist, und “alles” ist ein Begriff, der im Rahmen der naiven Mengenlehre nicht vorkommen darf.

Rechenregeln

Hier steht ∘ für ∪ oder ∩

Kommutativität: M∘N= N∘M
Assoziativität: K∘ (M∘N) = (K∘M) ∘N
Idempotenz: M∘M= M
Distributivität: K∪ (M∩N) = (K∪M) ∩ (K∪N) (und mit ∩ und ∪ vertauscht)

Übungen zu diesem Abschnitt

Ihr solltet euch wenigstens an den rötlich unterlegten Aufgaben versuchen

(1)

Seien A= {1,2,3,a,b}, B= {4,a} und C= A∪B.

Rechnet C, A∩B, ℘(B), A\B, B\A aus.

Antwort

(2)

Gilt ∅⊆∅, ist also die leere Menge ihre eigene Teilmenge?

Antwort

(3)

Wie ist das mit ∅⊂∅, ist also die leere Menge auch echte Teilmenge ihrer selbst? Tipp: Versucht, einen Beweis nach dem Muster des ∅⊆M-Beweises oben zusammenzuzimmern.

Antwort

(4)

Beweist mit Definitionen für Schnitt und Vereinigung sowie dem in einer Aufgabe zum Kapitel mit den logischen Aussagen bewiesenen “Distributivgesetz” für Junktoren, dass A∪ (B∩C) = (A∪B) ∩ (A∪C).