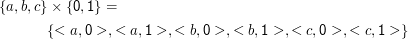Es gelten weiter:
Konsistenzprinzip:
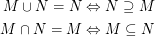
Adjunktivität: M∩ (M∪N) = M und mit ∩ und ∪ vertauscht.
DeMorgan:
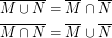
Einsehen über Venn-Diagramme

Man kann diese Sachen auch streng beweisen. Ein halbwegs strenges Beispiel: M∪N =M ∩N.
Zu zeigen “⊇”, also nach Definition: “Jedes Element von M ∩N ist auch Element von M∪N”. Sei also x∈M ∩N Dann ist nach der Definition der Schnittmenge x∈M und gleichzeitig x∈N, also nach Definition des Komplements x∉M und gleichzeitig x∉N, also ist mit einfacher Logik nicht x∈M oder x∈N, also nach Definition der Vereinigung x∉M∪N, also nach Definition des Komplements x∈M∪N.
Zu zeigen “⊆”, also nach Definition: “Jedes Element von M∪N ist auch Element von M ∩M. Sei also x∈M∪N. Dann ist nach Definition des Komplements x∉M∪N, also nach Definition der Schnittmenge x∉M und zugleich x∉N, also nach Definition des Komplements x∈M und zugleich x∈M, also nach Definition der Schnittmenge x∈M ∩N, q.e.d.”
Potenzmenge
Die Potenzmenge ℘(A) ist die Menge aller Teilmengen von A. Es gilt |℘(A)|= 2|A|, wobei |A| für die Zahl der Elemente in A steht. Beispiel: ℘({a,b}) = {∅,{a},{b},{a,b}}.
Wir haben die Zahl der Elemente einer Menge A als |A| recht nonchalant eingeführt. Wie so oft in der Mathematik ist das nicht ohne Fallen, denn niemand hat gesagt, dass man die Elemente einer Menge auch wirklich zählen kann – was wäre z.B. |ℕ|? Wir kehren unter dem Stichwort Kardinalität später nochmal zu dieser Frage zurück.
Kartesisches Produkt
M×N= {< m,n >|m∈M,n∈N}. heißt Kartesisches Produkt von M und N, dabei ist < m, n > ein Tupel.
Tupel sind anders als Mengen geordnet (d.h., < m,n >≠ < n,m >) und können einzelne Elemente öfter als ein Mal enthalten. Tupel mit zwei Elementen heißen auch Paare, solche mit drei und vier Tripel und Quadrupel, allgemein n-Tupel.
Der Begriff “kartesisch” bezieht sich auf René Descartes, der erkannte, dass mit einem Kartesischen Produkt der reellen Zahlen Punkte in der Ebene beschrieben werden können – zweidimensionale Koordinaten eben.
Beispiel: