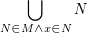8. Iteration in Zeichen

Häufig will man in der Mathematik Operationen auf eine Menge von Objekten durchführen – sie schneiden, vereinigen, addieren, was immer. Um so etwas elegant schreiben zu können, haben sich einige Schreibweisen entwickelt. Am häufigsten begegnet einem dabei die wiederholte Addition (Summe), während im Rahmen dieser Veranstaltung vor allem Mengenoperationen iteriert werden.

Seien n Größen a₁,a₂,…a_n gegeben. Wenn wir ihre Summe notieren wollten, könnten wir

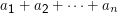
$a1 + a2 + ⋅⋅⋅ + an$

schreiben. Das ist aber lang und potenziell missverständlich. Mathematiker schreiben deshalb lieber:

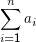
$∑n ai i=1$

Das funktioniert genau wie das gewohnte Plus. Man kann also ausklammern:

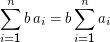
$∑n ∑n b ai = b ai i=1 i=1$

oder Summen umorganisieren:

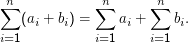
$∑n (ai + bi) = ∑n ai + ∑n bi. i=1 i=1 i=1$

Dabei ist natürlich wichtig, zu prüfen, was jeweils von der “Schleifenvariablen” i abhängt. In der ersten Regel ist b eine Konstante, in der zweiten sind die b_i für verschiedene i natürlich in der Regel verschieden. Es hilft am Anfang, die Summen auszuschreiben (zur Not für festes i) und mit Schulwissen nachzusehen, was geht und was nicht. So ist zum Beispiel

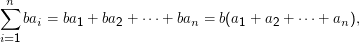
$n ∑ bai = ba1 + ba2 + ⋅⋅⋅ + ban = b(a1 + a2 + ⋅⋅⋅ + an), i=1$

und wir erkennen im zweiten Faktor des Ergebnisses unsere Summe wieder. Analog ist

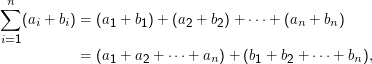
$∑n (ai + bi) = (a1 + b1) + (a2 + b2) + ⋅⋅⋅ + (an + bn ) i=1 = (a1 + a2 + ⋅⋅⋅ + an) + (b1 + b2 + ⋅⋅⋅ + bn),$

und wieder erkennen wir die Summen.

Die Zählvariable i kann natürlich auch anders heißen und muss nicht in Indizes verwendet werden, und die Grenzen müssen nicht 1 und n sein:

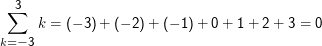
$3 ∑ k = (- 3) + (- 2) + (- 1) + 0 + 1 + 2 + 3 = 0 k= - 3$

Im letzten Beispiel hätte man unabhängig von den konkreten Grenzen schon vorhersagen können, dass die Summe Null ist, weil zu jeder negativen Zahl eine positive Zahl gleichen Betrags addiert wird. Argumente dieser Art heißen Symmetrieargumente und helfen sehr oft, die fraglichen Ausdrücke entscheidend zu vereinfachen.

Es gilt:

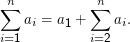
$∑n ∑n ai = a1 + ai. i=1 i=2$

und (jedenfalls, wenn 1 < m < n- 1):

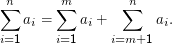
$∑n m∑ ∑n ai = ai + ai. i=1 i=1 i=m+1$

Übrigens ist es mitnichten nötig, dass der Summenindex im Ausdruck in der Summe vorkommt. Es ist etwa ∑ _i=1ⁿ1 = n⋅ 1. Wer das nicht glauben möchte, kann sich vorstellen, dass in Wirklichkeit ∑ _i=1ⁿ1i⁰ dasteht.

Analog zum Summenzeichen definieren Mathematiker gerne auch andere Mehrfachoperationen, etwa

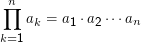
$∏n ak = a1 ⋅ a2 ⋅⋅⋅an k=1$

(das Zeichen kann als großes Pi gelesen werden und steht für Produkt in der gleichen Weise, in der das große Sigma für Summe steht),

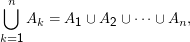
$⋃n Ak = A1 ∪ A2 ∪ ⋅⋅⋅ ∪ An, k=1$

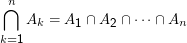
$⋂n A = A ∩ A ∩ ⋅⋅⋅ ∩ A k 1 2 n k=1$

oder

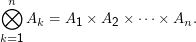
$⊗n Ak = A1 × A2 × ⋅⋅⋅ × An. k=1$

Für diese gelten natürlich andere Rechenregeln, so ist etwa

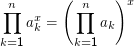
$( )x ∏n x n∏ ak = ak k=1 k=1$

Häufig braucht man eine etwas verallgemeinerte Notation, wenn die Objekte nicht einfach durchgezählt werden. Will man beispielsweise alle Elemente von M vereinigen, die x enthalten, kann man

$⋃ N N ∈M ∧x∈N$

schreiben.

Übungen zu diesem Abschnitt

Ihr solltet euch wenigstens an den rötlich unterlegten Aufgaben versuchen

(1)

Rechnet ∑ _i=1ⁿi für n= 2 bis n= 7 aus. Überlegt euch vorher, wie ihr das arbeitssparend hinbekommt (die Formel aus der nächsten Folie verwenden ist natürlich Betrug und in diesem Fall nicht mal arbeitssparend).

(2)

Was ist ∏ _i=1ⁿ(-1) in Abhängigkeit von n? Was ist ∑ _i=1ⁿ(-1)ⁱ?

Antwort

(3)

Wandelt ∑ _i=1ⁿ(a_i -a_i-1) in eine möglichst einfache Form um. Macht das dann auch noch mit ∏ _i=1ⁿ(a_i∕a_i-1).

Antwort

(4)

Sei M_n = {1,2,3,…,n}, also M₁ = {1}, M₂ = {1,2} und so fort.

Schreibt ⋂ _i=1³M_i und ⋃ _i=1³M_i aus und berechnet den Wert dieser Ausdrücke.