Eine Turingmaschine T= ⟨Φ,Σ,#,δ,S,F⟩ besteht aus
- Einem Alphabet von Zuständen Φ
- Einem Alphabet von Bandsymbolen Σ
- Einem Nullsymbol #
- Einer Übergangsfunktion
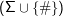δ: Φ ×
→Φ ×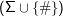
×{⊲,⊳,∘} - Einem Startzustand S∈Φ
- Einer Menge von Endzuständen F⊆Φ
Analog zu den Automaten lassen sich hier nichtdeterministische Varianten definieren, indem δ Werte in der Potenzmenge des hier verwendeten Wertebereichs nimmt. Wie endliche Automaten sind auch deterministische und nichtdeterministische Turingmaschinen äquivalent, solange wir keine Zeit- und Bandbeschränkungen haben.
Die Bandsymbole stehen auf einem Band, das “gespult” werden kann. Je nach dritter Komponente des Werts der Übergangsfunktion wird es nach links (⊲), rechts (⊳) oder gar nicht (∘) bewegt. Ein # steht für “Hier steht nichts” und kann als Begrenzungssymbol verwendet werden. Grundsätzlich ist das Band einer Turingmaschine aber unendlich. Das bedeutet, dass, wann immer der Lesekopf auf ein Feld kommt, das zuvor noch nicht berührt wurde, dort # steht.
Das erste Element des Werts der ÜF ist das zu schreibende Zeichen.
Die Übergangsfunktion einer Maschine, die nach links hin alles mit Einsen zukleistert, wäre demnach δ(z,#) = ⟨z,1,⊲⟩.
Im Unterschied zu einem Kellerautomaten kann die Turingmaschine überall im Speicher lesen und schreiben, und Speicher und “Eingabeband” sind identisch.