31. Kontextsensitive Sprachen

Eine Grammatik G= ⟨Φ,Σ,R,S⟩ heißt kontextsensitiv (oder vom Chomsky-1-Typ), wenn alle Regeln eine der beiden Formen

haben. Dabei ist A∈Φ, α,γ∈ (Σ ∪Φ)^* und β∈ (Σ ∪Φ)^*\{ϵ}. Falls < S,ϵ >∈R, darf weiter S nicht auf der rechten Seite einer Regel vorkommen.

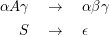
Kontextsensitive Grammatiken sind längenmonoton, d.h. die Länge von Wörtern in einer Ableitung nimmt nie ab.

Satz: Jede längenmonotone Sprache ist kontextsensitv.

Beweisidee: Das Problem sind hier lediglich Regeln, in denen mehr als ein Nonterminal ersetzt wird; diese lassen sich durch Einführung von “Zwischen-Nichtterminalen” aufteilen.

Man geht dabei schrittweise so vor, dass in jedem Schritt nur genau ein Nichtterminal ersetzt wird. Dazu führt man neue Nichtterminale ein, die nur genau im passenden Kontext ersetzt werden können. Eine Regel ABC → CAB könnte dabeiin folgende Regeln zerfallen: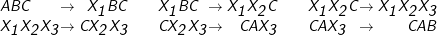

Wenn in Regeln dieser Art bereits auf der linken Seite Terminale stehen (z.B. aX → Xa), müssen für die betreffenden Terminale neue Nichtterminale eingeführt werden, die nach dem Muster der entsprechenden Manipulationen zur Wandlung kontextfreier Grammatiken in CNF dann in allen Regeln ersetzt werden.

Kontextsensitve Sprachen sind eine echte Obermenge kontextfreier Sprachen.

{aⁱ bⁱ aⁱ} ist nicht kontextfrei, kann aber durch folgende Regeln erzeugt werden:

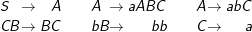
Bei Klabunde befindet sich hier ein subtiler Fehler: Er hat in der Regel A→abC ein großes B und dann zusätzlich eine Regel aB →ab. Dies führt zu Übergenerierung, da im Prinzip sofort alle C in a umgewandelt werden können und dann die zusätzliche Regel die B direkt in b umwandeln kann.

Beispielableitung: aabbaa

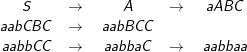
Man beachte, dass hinter dieser Grammatik schon eine regelrecht algorithmische Idee steckt: Wir sorgen zunächst dafür, dass immer nur aBC gemeinsam erzeugt werden und die keines der Nichtterminale verschwinden kann, bevor es zu einem Terminal wird. Dann bleibt das Problem, dass wir die B und C (die b und “rechten” a entsprechen) noch durchmischt haben.

Wir müssen also dafür sorgen, dass sie kontrolliert entmischt werden (und genau das geht mit kontextfreien Grammatiken nicht). Die Idee ist, dass wir, wenn wir genug a haben, das Nichtterminal A, das das Wachstum bewirkt, “sterilisieren” (das ist die Regel A →aBC) und dann anfangen, die C nach hinten zu treiben. Das geht einerseits durch die kontextsensitive Regel zur Vertauschung von B und C, andererseits durch den Zwang, ein B nur dann in ein b verwandeln zu können, wenn vor ihm ein b steht.

Chomsky-1-Grammatiken, die nicht ϵ erzeugen, können in die Kuroda-Normalform gebracht werden, in der alle Regeln eine der Formen

haben.

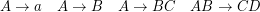
Erkennung von kontextsensitiven Sprachen durch Turingmaschinen.