30. Nutzen der CFGs

Kunstsprachen

Fast alle Programmiersprachen sind durch kontextfreie (meist LR(k)) Grammatiken beschrieben

Natursprachen

Umstritten – stärkstes Argument: CFGs sind das Komplexeste, das wir noch vernünftig beherrschen.

Klabunde S. 115: Schweizerdeutsch ist komplizierter als CFG. Man mag durchaus darüber diskutieren, wie viel solche Argumente wert sind. Zunächst nämlich sind Natursprachen de facto endlich (alle Äußerungen, über deren Richtigkeit man befinden müsste, müssen in finiter Zeit gemacht werden, und eigentlich dürfte schon unstrittig sein, dass “Sätze” oberhalb eine gewissen Länge als zumindest ungeschickt zurückgewiesen werden sollten). Daher ließen sie sich im Prinzip schon durch reguläre Sprachen modellieren. Die Frage ist, ob dies eine adäquate Beschreibungsweise ist, und diese Frage ist für reguläre Grammatiken auf jeden Fall mit Nein zu beantworten. Für kontextfreie Grammatiken sieht das anders aus – und durch geeignetes “Ausrollen” für einfache oder zweifache Verkreuzung lassen sich auch scheinbar kontextsensitive Sprachteile kontextfrei repräsentieren.

Aber: Zur Modellierung von Sprachteilen oder zum Teilparsen insbesondere in statistischen Verfahren reichen CFGs. Weitere Anwendungen in Morphologie, Phonetik, Semantik…

Wieder auf einem anderen Blatt steht, dass reine Phrasenstrukturgrammatiken nicht mehr als ernsthafte Modelle für die Modellierung von Natursprachen verwendet werden. In der Regel kommen irgendwelche Formen von Unifikation von außen dazu, häufig geht man auch ganz von der Phrasenstruktur ab und baut auf Dependenz; darin fungieren bestimmte Wörter als “Köpfe”, von denen dann wiederum andere Wörter “abhängen”. In solchen Formalismen ist die Beurteilung des Sprachtyps nicht immer ganz einfach (aber natürlich befinden sich die Sprachen irgendwo in der Chomsky-Hierarchie, denn die syntaktisch zulässigen Wörter (also Sätze) formen eine Menge, die prinzipiell auch mit Phrasenstrukturgrammatiken zu erzeugen wäre, nur eben mit weit unübersichtlicheren).

EBNF

EBNF (Extended Backus-Naur Form) ist Sprache zur Darstellung von kontextfreien Grammatiken. Jede EBNF-Klausel definiert eine Ersetzungsregel, die vorschreibt, wie ein Nichtterminalsymbol in andere Nichtterminalsymbole oder Terminalsymbole umgesetzt wird. Eine Regel sieht so aus:

ganzeZahl ::=

[vorzeichen ]ziffer { ziffer }

Eine ganze Zahl besteht aus einem optionalen Vorzeichen (die eckigen Klammern), einer Ziffer und null oder mehr weiteren Ziffern (die geschweiften Klammern). Die (kursiv geschriebenen) Nichtterminalsymbole vorzeichen und ziffer müssen noch erklärt werden. Das geht mit

ziffer ::=	"0"  | "1"  | "2"  | "3"  | "4"  |
	"5"  | "6"  | "7"  | "8"  | "9"  |
vorzeichen ::=	"+"  | "-"

In typewriter gedruckt sind Terminalsymbole , der vertikale Strich steht für “oder”. EBNF lediglich eine kompakte Darstellung unserer gewohnten Regelmengen. Die Regel für ganzeZahl z.B. ließe sich auch schreiben als:

wo G die Ganze Zahl, Z eine Ziffernfolge, V ein Vorzeichen und N eine Ziffer ist.

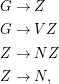
Mithin ist die Menge der durch Sätze von EBNF-Klauseln beschriebenen Sprachen gleich der Menge der kontextfreien Sprachen.

Vorsicht: Es gibt so viele Varianten von BNF und EBNF wie es AutorInnen gibt, die etwas damit ausdrücken. Häufige Varianten:

• Variation von “::=”
• Nichtterminale in spitzen Klammern
• Terminale ohne Anführungszeichen