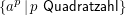Satz: Sei L eine kontextfreie Sprache. Dann gibt es eine Konstante n, so dass für jedes Wort z∈L, |z|≥n gilt:
- z= uvwxy
- |vx|≥ 1
- |vwx|≤n
- uviwxiy∈L für alle i≥ 0.
Beweis: Erzeuge G L, sei G in CNF. Da G binär verzweigend, können Ableitungsbäume der Höhe i höchstens Wörter der Länge 2i ableiten.
Sei n= 2|Φ|+1, d.h., mindestens ein Nichtterminal kommt mehr als einmal in der Ableitung vor. Sei |z|> n. Der Ableitungsbaum von z muss die Form

haben (die Seite, von der aus jeweils A abgeleitet wird, ist dabei natürlich egal, es könnte auch der linke Ast sein). Durch mehrmaliges Durchlaufen der Ableitung uAy * →uvAxy folgt die Behauptung.
Satz: L= {ai biai} ist nicht kontextfrei.
Beweis: Annahme: Behauptung falsch. Dann existiert ein z= anbnan mit n der Schranke aus dem PL und z= uvwxy.
Weil nach PL |vwx|≤n, kann vwx nur eine der Formen bl1, al1 (oBdA aus den linken a), al1bl2 oder bl1al2 haben. Dann hat aber uwy∈L (i= 0 im PL) eine der Formen anbn-l‘an, an-l‘bnan, an-l‘bn-l“an oder anbn-l‘an-l“, wobei l‘ ≤l1 und l“ ≤l2. Weil |vx|≥ 1, ist aber auch mindestens eines von l‘ und l“ größer als Null, und deshalb liegt keines dieser Wörter in L.
Aus dem Pumping Lemma folgt auch, dass Sprachen wie