28. Abschlusseigenschaften

Seien G_i = ⟨Φ_i,Σ_i,R_i,S_i⟩, i= 1,2 kontextfreie Grammatiken. Was passiert unter Vereinigung, Verkettung, Sternbildung, Durchschnitt, Komplement und Differenz der erzeugten Sprachen?

Vereinigung:

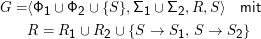
Verkettung:

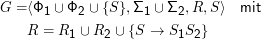
Sternbildung:

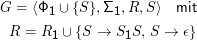
Durchschnitt: CFGs sind nicht abgeschlossen gegen Durchschnitt. Gegenbeispiel: L₁ = {aⁱbⁱa^j} und L₂ = {aⁱb^ja^j}. Der Schnitt der beiden Mengen ist {aⁱbⁱaⁱ}– dies ist nicht kontextfrei.

Komplement: Aus Abgeschlossenheit gegen Komplement würde Abgeschlossenheit gegen Durchschnitt folgen, deshalb sind CFGs auch nicht gegen Komplementbildung abgeschlossen.

Aus gegebenem Anlass die Schlussweise: Angenommen, L wäre kontextfrei. Dann würde aus der Kontextfreiheit von L₁ ∪L₂ die Kontextfreiheit von L₁ ∪L₂ und durch erneute Komplementbildung die von L₁ ∩L₂ folgen. Damit könnten wir aus der Abgeschlossenheit gegen Vereinigung die gegen Schnitt folgern – gegen Schnitt ist die Menge der kontextfreien Sprachen aber nicht abgeschlossen, Widerspruch.

Differenz: Komplement ließe sich auf Differenz zurückführen, deshalb: Wieder nicht abgeschlossen.