Die Wandlung von CFGs in Kellerautomaten wird einfacher, wenn wir auf Endzustände verzichten und Aktzeptanz durch leeren Keller definieren. Außerdem lassen wir “spontane” Übergänge zu (formal: Lesen von ϵ). Man müsste an dieser Stelle nachweisen, dass sich diese Sorte Kellerautomat in Kellerautomaten nach der ursprünglichen Definition umformen lässt und umgekehrt jeder “klassische” Kellerautomat einen äquivalenten Kellerautomaten dieses Typs hat – da die entsprechende Transformation aber recht haarig ist, wollen wir das einfach glauben.
Sei G= ⟨Φ,Σ,R,S⟩ kontextfrei. Der zugehörige Kellerautomat wird charakterisiert durch
- Das Kelleralphabet Δ = Φ ∪Σ,
- Das Kelleranfangssymbol S (d.h. das Startsymbol der Grammatik)
- Die Zustandsmenge ΦM = {z} (d.h. es gibt nur einen Zustand)
- Die Übergangsfunktion δ, wo für jede Regel A→α aus R ein Übergang ⟨z, ϵ, A⟩→< z,α > und außerdem ⟨z,a,a⟩→< z,ϵ > gesetzt wird.
Wir wandeln {S→b,S→aSa}; die Ü-Funktion ist:
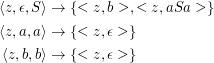
Test:
| ⟨z, aba,S⟩ | → | ⟨z,aba,aSa⟩ | → | ⟨z,ba,Sa⟩ | → |
| ⟨z, ba,ba⟩ | → | ⟨z,a,a⟩ | → | ⟨z,ϵ,ϵ⟩ | → ok |
| ⟨z, abba,S⟩ | → | ⟨z,abba,aSa⟩ | → | ⟨z,bba,Sa⟩ | → |
| ⟨z, bba,ba⟩ | → | ⟨z,ba,a⟩ | → boink |
Die Idee dieses Automaten ist eigentlich sehr einfach: Wenn wir oben auf dem Keller ein Nichtterminalsymbol haben, expandieren wir es mit irgendeiner passenden Regel (unsere Kellerautomaten sind ja nichtdeterministisch) und lesen nichts, wenn wir ein Terminalsymbol haben, entfernen wir es, wenn wir gerade das passende Terminalsymbol lesen.
Man kann diese Automaten natürlich zu “klassischeren” Kellerautomaten mit mehr Zuständen und ohne ϵ-Übergange reduzieren, aber so genau wollen wir es jetzt nicht wissen. Das Grundproblem – dass wir nämlich nichtdeterministische Kellerautomaten basteln – bleibt, es gibt kein Verfahren, das aus nichtdeterministischen Kellerautomaten deterministische macht.
Erzeugung einer Grammatik aus einem Automaten ist komplizierter. Im Wesentlichen kehrt man das Verfahren oben um und benutzt Tupel aus (Zustand-vor, Kellersymbol, Zustand-nach) als Nichtterminale der Grammatik.
Genauer bestehen die Tupel aus eine Zustand am Anfang eines Verarbeitungsschritts, dem Kellersymbol, das zu diesem Zeitpunkt ganz oben auf dem Keller liegt und dem Zustand, in dem der Automat ist, wenn der Keller kürzer wird als er am Anfang des Verarbeitungsschritts war.
Die Idee dabei ist, dass wir eine Regel ⟨z,A,z‘⟩ * →x genau dann einführen, wenn der zugehörige Kellerautomat durch die Eingabe x ggf. über mehrere Zwischenschritte, die natürlich ihrerseits Dinge auf den Keller legen und diese dann auch wieder runternehmen müssen, von z nach z‘ geht und A verarbeitet hat, also das Symbol unterhalb von A (das ja auf das, was der Automat auf dem Weg von z nach z‘ tut, keinen Einfluss haben kann) oben auf dem Keller liegt.
Wir gehen weiter von unseren modifizierten Kellerautomaten aus, wir akzeptieren also auf leeren Keller und lassen ϵ-Übergänge zu.
Ohne Beschränkung der Allgemeinheit können wir annehmen, dass unser Automat nie mehr als zwei Symbole auf einmal auf den Keller schiebt – das lässt sich durch Einführen zusätzlicher Zustände immer erreichen. Wir können dann folgende Regeln schreiben (darin stehen alle z und ihre Verzierungen für Elemente aus der Zustandsmenge, alle a, b, c mit Verzierungen für Elemente des Kelleralphabets, z0 ist der Startzustand, T ist das Startsymbol der Grammatik, S das Kelleranfangssymbol, gemäß unserer Definition oben):
- T→ ⟨z0,S,z⟩ für alle z aus der Zustandsmenge. ⟨z0,S,z⟩ ist das Symbol, aus dem alles ableitbar ist, was den Automaten dazu bringt, den Keller vom Kelleranfangssymbol aus zu leeren, d.h. eben alle Elemente der Sprache.
- ⟨z, a‘,z‘⟩→a, wenn in der Ü-Funktion ⟨z,a,a‘⟩→< z‘,ϵ > steht. Die sind einfach: Die Maschine nimmt ein a‘ vom Stack und liest ein a. Dazwischen kann nichts passieren, und sie muss im Zustand z‘ enden. Aus ⟨z,a‘,z‘⟩ kann also nur a werden.
- ⟨z,a‘,z‘⟩→a⟨z1,b,z‘⟩ für alle z‘ ∈Φ, wenn in der Ü-Funktion ⟨z,a,a‘⟩→< z1,b > steht. Das ist schon kitzliger: Der Automat nimmt a‘ vom Keller und legt b drauf, liest derweil aber a. Damit müssen wir, um zu sehen, as ⟨z,a‘,z‘⟩ so werden kann, erstmal ein a haben und dann sehen, was wir alles machen können, wenn wir von z1 irgendwo anders hingehen. Wesentlich ist aber, dass beim zweiten Schritt am Anfang das b auf dem Keller liegt, das beim Übergang z→z1 dort landet.
- ⟨z, a‘,z‘⟩→a⟨z1,b,z2⟩⟨z2,c,z‘⟩ für alle z‘,z2 ∈Φ, wenn in der Ü-Funktion ⟨z,a,a‘⟩→< z1,bc > steht. Das lässt sich analog zum letzten Fall einsehen, nur müssen wir dieses Mal zwei Symbole vom Keller nehmen und haben also zwei Mal die Freiheit, das in irgendwelchen geeigneten Zuständen des Automaten zu tun.
Das sieht konfus und willkürlich aus, wäre aber eigentlich einfach, wenn man beim Nachdenken drüber nicht leicht den Überblick verlieren würde. Wer sehen will, warum das so aufgeht, kann den Beweis bei Schöning goutieren – im Wesentlichen muss man nur per Induktion zeigen, dass die Grammatik in jedem Ableitungsschritt genau das produziert, was der zugehörige Automat mit den durch die Symbole der Grammatik beschriebenen Schritten verbraucht.
Als Beispiel nehmen wir den Automaten oben:
| ⟨z,ϵ,S⟩ | → | < z,b > | ⟨z,ϵ,S⟩ | → | < z,aSa > | |
| ⟨z,a,a⟩ | → | < z,ϵ > | ⟨z,b,b⟩ | → | < z,ϵ > |
Zunächst führen wir einen neuen Zustand ein, so dass nie mehr als zwei Symbole auf den Stack gepusht werden (die Spitze des Stacks soll wieder vorne sein):
| ⟨z,ϵ,S⟩ | → | < z,b > | ⟨z,ϵ,S⟩ | → | < y,Sa > | ⟨y,ϵ,S⟩ | → | < z,aS > | |
| ⟨z,a,a⟩ | → | < z,ϵ > | ⟨z,b,b⟩ | → | < z,ϵ > |
Sehen wir zunächst, wohin wir vom Startzustand aus kommen (Regeln vom Typ 1):

Als nächstes verarbeiten wir die Regeln vom Typ (2), Suchen also alle Übergänge, die auf < z,ϵ > enden. Dabei haben wir jeweils z= z, z‘ = z und einmal a‘ = a= a und einmal a‘ = a= b (dabei kommen die Symbole rechts jeweils aus unserem Kellerautomaten, die links aus der Regeldefinition). Wir erhalten die folgenden Regeln:

Für die Regeln vom Typ (3) brauchen wir die Übergänge, die ein Zeichen am Keller hinterlassen. Davon haben wir nur eine, und für diese ist (mit der Konvention aus dem letzten Absatz) z= z, a= ϵ, a‘ = S, z1 = z, b= b. In unserer Zustandsmenge befinden sich z und y, wir erhalten also die folgenden beiden Regeln:

Soweit wars einfach. Für die Regeln des Typs (4) müssen wir ernsthaft arbeiten. Bei ⟨z,ϵ,S⟩→< y,Sa > ist z= z, a= ϵ, a‘ = S, z1 = y, b= S und c= a. Wir müssen sowohl z‘ als auch z2 über beide Zustände iterieren, erhalten also vier Regeln:
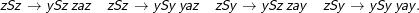
Für den anderen Übergang dieses Typs haben wir z= y, a= ϵ, a‘ = S, z1 = z, b= a und c= S und erhalten analog die Regeln
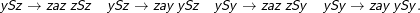
Das hat keine große Ähnlichkeit mit der Ausgangsgrammatik. Wir können aber einen Haufen Regeln wegwerfen, wenn wir bedenken, dass Regeln, auf deren linker Seite etwas steht, was in keiner Regel auf der rechten Seite vorkommt, nie in einer Ableitung vorkommen können, die bei T anfängt und umgekehrt Regeln, in denen Nichtterminale vorkommen, die nie zu Terminalen werden können, ebenfalls nicht in Ableitungen von Wörtern vorkommen können. Mit letzterem Argument kann man alle Regeln streichen, die yaz, yaz, yay oder zay enthalten. Damit ist dann aber auch ySy nicht mehr erreichbar, so dass auch die Regel mit diesem Nichtterminalsymbol auf der linken Seite gestrichen werden kann.
Übrig bleiben
| T | → | zSz | T | → | zSy | zaz | → | a | zbz | → | b | |
| zSz | → | zbz | zSy | → | zby | zSz | → | ySz zaz | ySz | → | zaz zSz |
Das ist immer noch ziemlich viel, lässt sich aber weiter vereinfachen, indem man die eigentlich überflüssigen Nichtterminale zSy, zaz und zbz durch Einsetzen eliminiert:
| T | → | zSz | T | → | b | zSz | → | b | zSz | → | ySz a | ySz | → | a zSz |
Jetzt kann man noch fleißig Regeln ineinander einsetzen und erhält die Ausgangsgrammatik
| T | → | a T a | T | → | b |
LR-Sprachen
Die Mengen der von deterministischen (|δ(z,a,A)|+ |δ(z,ϵ,A)|≤ 1) und von nichtdeterministische Kellerautomaten akzeptierten Sprachen sind verschieden.
Die von deterministischen Kellerautomaten akzeptierten Sprachen sind die LR(k)-Sprachen; sie sind eine Untermenge der kontextfreien Sprachen und können geparst werden, ohne jemals weiter als k Zeichen vorauszuschauen (bei allgemeinen CFGs können im Prinzip beliebig lange Sackgassen auftreten).