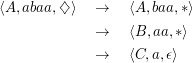26. Kellerautomaten und CFGs

Satz: Zu jeder CFG G gibt es einen Kellerautomaten, der L(G) akzeptiert, und zu jedem Kellerautomaten A gibt es eine CFG, die L(A) erzeugt.

Der Beweis ist aufwändig. Zunächst Beispiel: {aⁱbaⁱ} wird akzeptiert von folgendem Kellerautomaten:

Beispielableitungen: Wir leiten b ab:

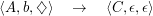
$⟨A, b,♢ ⟩ → ⟨C,ϵ,ϵ⟩$

Wir leiten aabaa ab:

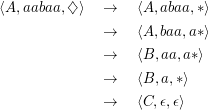
$⟨A, aabaa,♢ ⟩ → ⟨A, abaa,* ⟩ → ⟨A, baa,a* ⟩ → ⟨B, aa,a *⟩ → ⟨B, a,*⟩ → ⟨C, ϵ,ϵ⟩$

abaa wird zurückgewiesen:

$⟨A, abaa,♢ ⟩ → ⟨A, baa,*⟩ → ⟨B, aa,* ⟩ → ⟨C, a,ϵ⟩$

– kein gültiger Endzustand, da restliche Eingabe ≠ϵ.