Auch bei kontextfreien Grammatiken würden wir gerne das Wortproblem lösen. Endliche Automaten reichen dazu aber garantiert nicht aus, weil sie genau die regulären Sprachen erkennen, es aber kontextfreie Sprachen gibt, die nicht regulär sind.
Die Lösung des Wortproblems für kontextfreie Sprachen führt ziemlich schnell zu den klassischen Parsern, die neben der Information, ob ein Wort Element einer Sprache ist oder nicht auch noch z.B. Parsebäume erzeugen. Das ist eine Theorie für sich, die z.B. in unserer Parsing-Veranstaltung oder auch in Compilerbau-Vorlesungen der Informatik ausgebreitet wird.
Man braucht aber keinen “vollständigen” Computer, um das Wortproblem für kontextfreie Sprachen zu lösen – tatsächlich reicht schon eine eher kleine Erweiterung der DEAs.
Ein (nichtdeterministischer) Kellerautomat ist ein Tupel K= ⟨Φ,Σ,Δ,♢,δ,S,F⟩ aus
- Einem Alphabet Φ von Zuständen
- Einem zu Φ disjunktem Alphabet Σ von Eingabesymbolen
- Einem zu Φ disjunktem Alphabet Δ von Kellersymbolen
- Einem Kelleranfangssymbol ♢
- Einer Übergangsfunktion δ:Φ ×Σ × (Δ ∪{♢}) →℘(Φ ×Δ*)
- Einem Startzustand S∈Φ
- Einer Menge von Endzuständen F⊆Φ.
Ein Übergang in einem Kellerautomat wird als
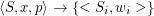
Eine Konfiguration ⟨T,v,p⟩ besteht aus
- Einem Zustand T∈Φ (dem augenblicklichen Zustand)
- Einem Wort v∈Σ* (dem noch nicht gelesenen Teil des Eingabeworts)
- Einem Wort p∈Δ*∙{♢} (dem augenblicklichen Kellerinhalt)
Die Startkonfiguration eines Kellerautomaten hat immer die Form ⟨S,w,♢⟩, eine Endkonfiguration ⟨T,ϵ,z⟩ mit z∈Δ*∙{♢} und T∈F.
Eine äquivalente Definition verzichtet auf Endzustände und definiert Akzeptanz durch den Kellerzustand am Wortende (z.B. Keller leer).
