Eine Grammatik heißt 1-frei, wenn sie keine Regeln der Form A→B (A,B∈Φ – 1-Regeln) enthält.
Satz: Sei G eine kontextfreie Grammatik. Dann gibt es eine 1-freie Grammatik G‘, so dass L(G) = L(G‘) (die Grammatiken sind schwach äquivalent).
Beweis: Die Grundidee dieser Umformung ist: Wenn ich zwei Regeln A→B und B→x habe, führe ich eine neue Regel A→x ein und brauche dann kein A→B.
Im Allgemeinen allerdings muss man etwas genauer aufpassen. Das erste Problem sind Zyklen: Damit ist gemeint, dass durchaus A→B und B→A gemeinsam in einer Regelmenge vorkommen können. Ein naives Ersetzen würde damit in eine Endlosschleife führen. Die Lösung ist einfach: Alle Nichtterminale in einem Zyklus sind äquivalent und können (in allen Regeln!) durch ein einziges Nichtterminalsymbol ersetzt werden.
Die restlichen 1-Regeln lassen sich nach dem Algorithmus
entfernen.Solange noch 1-Regeln in der Regelmenge enthalten sind:
Wähle eine 1-Regel r (sagen wir A→B), so dass es keine 1-Regel mit B auf der linken Seite gibt: Für alle Regeln B→α:Führe eine neue Regel A→α einEntferne r.
Die Forderung, B solle in keiner 1-Regel auf der linken Seite vorkommen, verhindert, dass bei diesem Verfahren neue 1-Regeln entstehen. Dass diese Forderung immer für mindestens eine 1-Regel erfüllbar ist, liegt daran, dass wir Zyklen schon im Vorfeld eliminiert haben.
Um zu sehen, wie das geht, können wir die Regelmenge
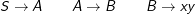
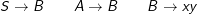
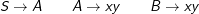
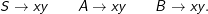
Natürlich braucht es jetzt die Regeln mit A und B auf der linken Seite nicht mehr. Aber dazu später.
Eine kontextfreie Grammatik heißt ϵ-frei, wenn sie keine Regeln der Form A→ϵ enthält (⇒ Wörter in Ableitungen werden nie kürzer).
Satz: Wenn ϵ∉L(G), gibt es eine zu G schwach äquivalente ϵ-freie Grammatik.
Beweis: Zunächst alle Ai ∈Φ mit Ai
*
→ϵ in V sammeln (zuerst alle A
i mit Ai →ϵ, dann alle Ai mit
Ai →Ak1
Akn, wo alle Akj ∈V). Dann alle Ai →ϵ-Regeln entfernen und für jede Regel B→xAiy mit xy≠ϵ und
Ai ∈V eine Regel B→xy hinzufügen.
Eine Grammatik ist in Chomsky-Normalform (CNF), wenn alle Regeln eine der Formen
- A→a
- A→BC
Satz: Sei G eine kontextfreie Grammatik mit ϵ∉L(G). Dann gibt es eine kontextfreie Grammatik G‘ in CNF mit L(G) = L(G‘).
Beweis: oBdA G ϵ-frei und 1-frei. Wir konstruieren G‘ = ⟨Φ‘,Σ‘,R‘,S‘⟩.
- Regeln A→a werden nach R‘ übernommen
- Für alle Terminalsymbole xi auf der rechten Seite, die nicht alleine stehen, werden Regeln Cxi →xi eingeführt und die xi in den Regeln durch Cxi ersetzt.
- Die restlichen Regeln haben die Form A→Y 1…Y n. Wenn n≠2, werden weitere Nichtterminale Zi eingeführt, so dass A→Y 1Z1 bis Zn-2 →Y n-1Y n.
Nach der Umwandlung in CNF kann die Grammatik in der Regel noch “aufgeräumt” werden.
Dazu werden Symbole, die vom Startsymbol aus nicht in einer Ableitung zu einem nur aus Terminalen bestehenden Wort führen, aus Φ und Terminale, die nicht erzeugt werden können, aus Σ entfernt.
Man kann das algorithmisch formulieren, wir bescheiden uns mit Intuition – Nichtterminale, die nie auf der linken Seite einer Regel auftreten, können offenbar nie aus Wörtern verschwinden; solche Wörter können, da sie ein Element von Φ enthalten, dann auch nie Wörter aus L(G) ⊆Σ* sein. Demnach darf man alle Regeln, die sie erwähnen, entfernen. Darurch können natürlich weitere Nichtterminale nicht mehr auf der linken Seite auftauchen. Kommen zwei Terminale nur mit jeweils identischen rechten Seiten vor, können sie verschmolzen werden.
Ein Beispiel: Vorgelegt sei die Regelmenge
| A | → | aCD | B | → | bCD | C | → | D | |
| C | → | ϵ | D | → | C | S | → | ABC |
Wir wollen sie in CNF umformen, machen sie also ϵ-frei. Zunächst ist C in der Menge der auf ϵ führenden Symbole, wegen D → C aber auch D. Wir ergänzen die Regelmenge und werfen die ϵ-Regel raus:
| A | → | a | A | → | aC | A | → | aCD | A | → | aD | |
| B | → | b | B | → | bC | B | → | bCD | B | → | bD | |
| C | → | D | D | → | C | S | → | AB | S | → | ABC |
Im nächsten Schritt eliminieren wir Zyklen. Davon gibt es hier nur einen, nämlich zwischen C und D. Wir vereinigen die beiden Symbole zu einem neuen Symbol E (was hier nur der Klarheit halber geschieht – natürlich hätten wir auch einfach alle D durch C ersetzen können):
| A | → | a | A | → | aE | A | → | aEE | B | → | b | |
| B | → | bE | B | → | bEE | S | → | AB | S | → | ABE |
Jetzt haben wir keine 1-Regeln mehr, können also mit der Prozedur aus dem Beweis anfangen. Wir haben zwei Terminale, die mit Nichtterminalen zusammenstehen, nämlich a und b. Glücklicherweise brauchen wir dafür keine neuen Nichtterminale einzuführen, weil bereits A und B diese beiden erzeugen:
| A | → | a | A | → | AE | A | → | AEE | B | → | b | |
| B | → | BE | B | → | BEE | S | → | AB | S | → | ABE |
Wir haben jetzt noch drei Regeln mit drei Nichtterminalen auf der rechten Seite, alle anderen Regeln sehen schon aus wie in CNF gewünscht. Wir führen ein Nichtterminal für EE ein, für AB haben wir schon eins:
| A | → | a | A | → | AE | A | → | AF | B | → | b | F | → | EE | |
| B | → | BE | B | → | BF | S | → | AB | S | → | SE |
Das ist jetzt schon in CNF, aber komplizierter, als es sein muss, wie deutlich wird, wenn wir nicht verwendete Symbole rauswerfen. Insbesondere wird E nicht verwendet, weil es nie auf der linken Seite einer Regel vorkommt. Damit sind auch alle Regeln, die E enthalten, überflüssig, weil sie am Ende immer auf ein Wort mit E führen würden, also nie ganz Terminal werden könnten; da die Regel F → EE wegfällt, gilt dies auch für F. Unsere Anfangsgrammatik in CNF und reduziert ist also platterdings:
| A | → | a | B | → | b | S | → | AB |
Also kleine Anmerkung am Rande: Diese Sprache ist endlich und damit sogar regulär. In der Tat reicht S→ab als Regelmenge aus (aber das wäre natürlich nicht mehr in CNF).