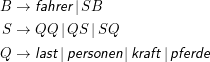Eine Grammatik G= ⟨Φ,Σ,R,S⟩ heißt kontextfrei oder Chomsky-2-Grammatik, wenn jedes Element von R die Form A→α hat mit A∈Φ und α∈ (Σ ∪Φ)*.
Kontextfreie Grammatiken schließen trivial reguläre Grammatiken ein, sind aber eine echte Obermenge.
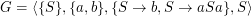
Ableitungen in kontextfreien Grammatiken sind nicht eindeutig. Sei
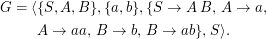
aab kann abgeleitet werden:
| (1) | S | → | AB | → | aaB | → | aab |
| (2) | S | → | AB | → | Ab | → | aab |
| (3) | S | → | AB | → | aB | → | aab |
Zwei Phänomene: (1) und (2) sind verschieden abgeleitet, führen aber auf gleiche Bäume, (1) und (3) führen auf verschiedene Bäume.
Lösung für (1) vs. (2): Linksableitungen. Eine Linksableitung ist eine Ableitung, bei der immer das am weitesten links stehende Nichtterminal ersetzt wird. Offenbar gibt es zu jeder Ableitung eine zugehörige Linksableitung, wir verlieren also nichts, wenn wir diese Einschränkung machen.
Analoge Probleme können in einseitig linearen Grammatiken nicht auftreten, weil in den Wörtern, die während einer Ableitung auftreten, per definitionem immer nur ein Nichtterminal steht (und zwar entweder ganz links oder ganz rechts).
Linksableitungen und Ableitungsbäume entsprechen sich eindeutig. Dass eine Ableitung eindeutig einen Baum bestimmt, hatten wir bereits ganz am Anfang gesehen. Um umgekehrt aus einem Ableitungsbaum eine Linksableitung zu erzeugen, fängt man bei der Wurzel an und wertet jeweils den am weitesten links oben stehenden noch unbearbeiteten Knoten aus.
(1) vs. (3) ist nicht “lösbar”, die Zweideutigkeit liegt hier in der Natur kontextfreier Grammatiken.
Eine kontextfreie Grammatik heißt ambig, wenn es für mindestens ein w∈L(G) mehrere Linksableitungen S * →w gibt, eindeutig sonst. Eine kontextfreie Sprache heißt ambig, wenn jede sie erzeugende kontextfreie Grammatik ambig ist.
Ambiguität ist eigentlich nicht schlecht – sie taucht in der natürlichen Sprache überall auf:

Hier wurde der Satz “Erna steuert das Auto mit dem Lenkrad” mit einer hypothetischen Gammatik des Deutschen geparst. Dabei sind zwei Lesungen denkbar – entweder, Erna verwendet das Lenkrad, um das Auto zu steuern, oder das Auto, das sie fährt, hat ein Lenkrad und nicht etwa einen Joystick oder einen Steuerknüppel oder etwas ähnliches.
Ambiguitäten dieser Art sind typisch für die natürliche Sprache. Dass wir Menschen meistens doch recht gut wissen, was gemeint ist, liegt vor allem an semantischen Informationen, zumal in Sprachen mit deutlich ärmerer Morphologie. Eine gute Demontration dieses Effekts ist das Satzpaar “time flies like an arrow” und “fruit flies like a banana” (wers nicht sieht: “fruit flies” sind hier Fruchtfliegen). Ohne Wissen, was Zeit, Pfeile, Fruchtfliegen und Bananen sind, ist ein Parser hier aufgeschmissen.
Tatsächlich sind Ambiguitäten in “klassischen” Phrasenstrukturgrammatiken (also Grammatiken, die so beschrieben sind, wie wir das hier machen) ein riesiges Problem, denn es ist nicht ungewöhnlich, dass Sätze mit ein paar dutzend Wörtern ohne weitere Information auf Millionen von Bäumen führen. Unter anderem diese Feststellung hat zur Einsicht geführt, dass ohne Anleihen aus den stark lexikalisierten Dependenzgrammatiken bei der Verarbeitung natürlicher Sprache kaum etwas zu gewinnen ist. Aber das ist ein Thema für die Syntax-Veranstaltung.