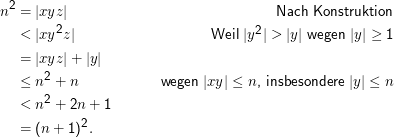22. Reguläre Sprachen II

Satz: Ist L eine reguläre Sprache, so gibt es einen endlichen Automaten A, der L akzeptiert.

Beweis: Wieder konstruktiv über die fünf Eigenschaften regulärer Sprachen.

(1) ∅ wird von allen Automaten ohne Endzustände erzeugt

(2) Einzelne Zeichen aus dem Alphabet gehen mit

wenn nur B ein Endzustand ist – d.h., das gesuchte Zeichen treibt den Automaten in den Endzustand, jedes andere oder ein weiteres in einen nicht-akzeptierenden.

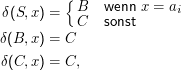
(3) Vereinigung: Φ₁ und Φ₂ disambiguieren wie gehabt, einen neuen Startzustand machen, der als Folgezustände die Folgezustände der alten Startzustände hat. Das geht, weil nicht zwischen Φ₁ und Φ₂ gesprungen wird. Der neue Startzustand muss in die neuen Endzustände aufgenommen werden, wenn einer der alten Startzustände Endzustand war.

(4) Verkettung: Startzustand von A₁ wird neuer Startzustand, alle Endzustände von A₁ werden mit den Startzuständen von A₂ vereinigt (und nicht in F aufgenommen, es sei denn Startzustand von A₂ ist in F₂), Endzustände sind F₂

(5) Sternbildung: Startzustand wird zu Endzustand (wg. ϵ). Dann alle Endzustände wieder auf Startzustand verweisen lassen.

Diesen Satz hätten wir eigentlich gar nicht mehr beweisen müssen. Aus der Äquivalenz von einseitig linearen Grammatiken und regulären Ausdrücken auf der einen und der zwischen einseitig linearen Grammatiken DEAs auf der anderen Seite folgt nämlich sogar die Äquvialenz von DEAs und regulären Ausdrücken.

Abschlusseigenschaften

Da Sprachen zunächst nur Mengen sind, kann man durch die üblichen Mengenoperationen neue Sprachen erzeugen – es wäre beispielsweise toll, wenn man eine Grammatik für Hauptsätze hätte und eine für Relativsätze und durch Vereinigung eine Grammatik bekäme, die beides abdeckt. Die Frage ist aber: gibt es für die – in diesem Fall – vereinigte Menge immer noch eine – beispielsweise – reguläre Grammatik?

Seien L₁, L₂ zwei reguläre Sprachen. Dann sind L₁ ∙L₂, L₁ ∪L₂ und L_i^* trivial regulär.

Σ^* \L=L ist regulär: Es existiert ein Automat A= ⟨Φ,Σ,δ,S,F⟩, der L akezptiert. Der Automat A‘ = ⟨Φ,Σ,δ,S,Φ \F⟩ akzeptiert genau alle Wörter nicht, die A nach F treiben und endet für alle anderen in einem Endzustand, akzeptiert also L. Daher muss L regulär sein

L₁ ∩L₂ =L₁ ∪L₂ (deMorgan), Regularität ist aber unter Vereinigung und Komplementbildung erhalten.

L₁ \L₂ = L₁ ∩L₂, also auch regulär.

Das Pumping Lemma

Satz: Zu jeder regulären Sprache L existiert eine Zahl n, so dass sich alle w∈L mit |w|≥n als w= x∙y∙z darstellen lassen mit

• x,y,z∈Σ^*
• |y|≥ 1
• |x∙y|≤n
• x∙yⁱ ∙z∈L.

Beweis: Der entscheidende Punkt ist die vierte Bedingung. Weil L regulär, gibt es einen Automaten A mit Zuständen T _i (i= 1,…,n), der L akzeptiert.

Wenn es kein w mit |w|≥n gibt, ist nichts zu beweisen. Sei also |w|≥n. Dann wird mindestens ein T_k mehrfach durchlaufen. Wir zerlegen w, so dass

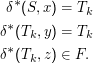
Durch triviale Induktion folgt damit, dass auch x∙yⁱ ∙z in von A akzeptiert und damit in L ist.

In Prosa: Wörter in ausreichend komplexen regulären Sprachen lassen sich “normalerweise” aufblasen. Deshalb lassen sich balancierte Klammern nicht mit regulären Ausdrücken prüfen:

Satz: L= {aⁱbaⁱ} ist nicht regulär.

Beweis: Annahme: L ist regulär. Sei i, so dass z= aⁱbaⁱ länger als n aus dem Pumping Lemma ist. Dann gibt es eine Zerlegung z= uvw mit v≠ϵ. Da nach Pumping Lemma auch uv^jw∈L, ist kein b in v. Also muss v= a^l mit l > 0 sein. Damit liegt auch a^i+lbaⁱ (wenn b in w ist) oder aⁱba^i+l (sonst) in L, Widerspruch.

Satz: L= {a^p|p Quadratzahl} ist nicht regulär.

Beweis: L enthält auf jeden Fall Wörter, die länger als n aus dem Pumping Lemma sind. OBdA n > 1. Sei nun speziell p= n². Dann ist w= xyz und |xy|< n sowie |y|≥ 1 nach Pumping Lemma. Außerdem ist xy²z∈L (Vorsicht: Hier haben wir zwei Bedeutungen der Potenz: In n² bedeutet es das gewohnte Quadrat, in y² die Verkettung).

Jetzt ist

Damit liegt |xy²z| zwischen zwei aufeinanderfolgenden Quadratzahlen, kann also selbst keine Quadratzahl sein.