21. Transducer

Eine Transducer ist ein “Automat mit Drucker”, genauer ein Tupel ⟨Φ,Σ_i,Σ_o,δ,λ,S⟩ mit

Einem Zustandsalphabet Φ
Einem Eingabealphabet Σ_i
Einem Ausgabealphabet Σ_o
Einer Übergangsfunktion δ:Φ ×Σ_i →Φ
Einer Ausgabefunktion λ:Φ ×Σ_i →Σ_o^*
Einem Startzustand S∈Φ

Gegenüber einem DEA kommen also Σ_o und λ dazu.

Alternativ könnte man auch die Übergangsfunktion eines DEA zu einer Funktion δ:Φ ×Σ_i →Φ ×Σ_o^* erweitern. Dann ist natürlich λ nicht mehr nötig.

Endliche Transducer sind ein Konzept, das in der Sprachverarbeitung eine wichtige Rolle spielt – klassisch ist etwa die Two-Level-Morphology, eine der verbreitetsten Methoden für die Computermorphologie.

Man kann endliche Transducer auch auffassen als einen Automaten, der auf Paaren von Eingabesymbolen läuft, der sozusagen von zwei Eingabebändern liest, und zwar so, dass der äquivalente “Standard-Transducer” (bei vielen Autoren ist Standard und Variante dabei gegenüber unserer Definition vertauscht) bei Eingabe des einen Bandes gerade das andere als Ausgabe erzeugt. Der so entstandene DEA akzeptiert eine Folge von Paaren von Eingabesymbolen genau dann, wenn die Folge der ersten Elemente der Paare den Transducer zur Ausgabe der zweiten Elemente bringen würde. In diesem Sinn kann man Transducer mit endlichen Automaten simulieren, woraus auch folgt, dass Ein- und Ausgaben endlicher Transducer zusammen eine reguläre Sprache bilden.

Ein Grund für die breite Anwendung von Transducern liegt in den Abschlusseigenschaften der regulären Sprachen: Transducer lassen sich sehr einfach verketten, vereinigen, komponieren usf. Die fsmtools bieten einen fertig durchprogrammierten Werkzeugkasten dazu.

Die Paradeanwendung von Transducern in der Computerlinguistik ist die Morphologie, in der Transducer etwa zur Produktion von Wortformen dienen. Hier ein Beispiel, wie so ein Transducer aussehen könnte:

Dieser Transducer kann aus “Tiefenstrukturen” wie spring+3p (“springen in der 3. Person Plural”) oder spring+pt (“springen in 3. Person Singular Präteritum”) “Oberflächenstrukturen” wie “springen” oder “sprang” machen. Es ist schon aus diesem beliebig vereinfachten Beispiel klar, dass solche Transducer nur maschinell generierbar sind. Eingebeformalismen für diese Generierung gibt es etliche – mit der bekannteste wurde durch das Urkimmo-System definiert. Bei dieser Generierung wird gleich noch dafür gesorgt, dass die resultierenden Transducer deterministisch sind und nicht wie hier nichtdeterministisch.

Ähnlich lassen sich Transducer definieren, die aus einem Text nach gewissen Regeln – letztlich natürlich regulären Ausdrücken – bestimmte “interessante” Konstrukte herausfischen, beispielsweise Eigennamen. Dabei operieren die Transducer dann meistens nicht mehr auf einzelne Zeichen, sondern auf morphosyntaktische Merkmale der einzelnen Wörter (meist so genannte Tags, die zu jedem Wort eine irgendwie definierte Wortklasse angeben).

Ein weiteres Beispiel ist die Addition im Binärsystem. Wir stellen Zahlen dar als …b₂b₁b₀ mit b_i ∈{0,1} und z= ∑ b_i2ⁱ (binäre oder 2-adische Darstellung). Addition in Binärdarstellung einfach:

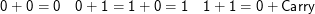
$0 + 0 = 0 0 + 1 = 1 + 0 = 1 1 + 1 = 0 + Carry$

Carry heißt so viel wie Übertrag – es entspricht dem “Merke eins” aus der Grundschuladdition. Wir müssen also noch jeweils sagen, was passiert, wenn wir einen Übertrag haben. Auch das ergibt sich sehr einfach:

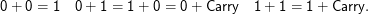
$0 + 0 = 1 0 + 1 = 1 + 0 = 0 + Carry 1 + 1 = 1 + Carry.$

Wir brauchen einen Automaten, der ein 2-Tupel von Bits < b_1,i,b_2,i > liest und je nach Tupel entweder 0 oder 1 ausgibt und zusätzlich ein Carry verwalten kann.

Eine Beispielberechnung: 35 = 14 + 21 = 01110₂ + 10101₂. Die Maschine erwartet die Eingabe “Least significant bit first”, also rückwärts. Das Eingabewort ist also

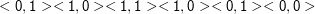
$< 0,1 > < 1, 0 > < 1,1 > < 1,0 >< 0,1 >< 0,0 >$