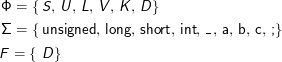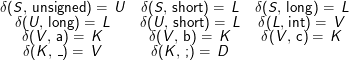20. Automaten können reguläre Sprachen

Satz: Jede von einem DEA akzeptierte Sprache ist regulär.

Beweisidee: Konstruiere aus DEA ⟨Φ,Σ,δ,S,F⟩ die Grammatik G= ⟨Φ,Σ,R,S⟩, wobei die Regelmenge

ist. Korrekterweise muss jetzt noch per Induktion über die Wortlänge nachgewiesen werden, dass S * →wT⇔δ^*(S,w) = T – ggf. Klabunde, 59.

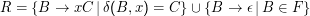
Umkehrung lässt sich leider nicht so direkt zeigen; Gegenbeispiel:

Beim dem Lesen von “vielleicht” müsste sich der Automat entscheiden, ob er nach A oder B gehen und dann entweder nur “ja” (im Fall A) oder “nein” (im Fall B) akzeptieren soll. Die ÜF eines DEA muss aber zu jedem Eingabezeichen eindeutig den nächsten Zustand geben.

Überlegt man sich, dass die mit diesen Regeln erzeugte Sprache

ist, ist es nicht schwer, folgenden DEA zu konstruieren, der L(G) akzeptiert:

Das Problem ist nur, dass wir nicht wissen, ob sowas wirklich immer geht, ganz abgesehen davon, dass wir ohnehin lieber ein systematisches Verfahren hätten, aus beliebigen einseitig linearen Grammatiken DEAs zu machen. Dazu nehmen wir einen Umweg:

NDEAs

Abhilfe: Nichtdeterministische endliche Automaten. Diese sehen aus wie DEAs, nur ist das Startsymbol jetzt eine Teilmenge von Φ und

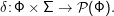
Außerdem dürfen NDEAs natürlich auch mehrere Startzustände haben. Man kann sich vorstellen, dass ein NDEA systematsich alle Möglichkeiten durchprobiert, wenn er mehrere mögliche Folgezustände hat. Meist ist aber einfacher, sich vorzustellen, der NDEA habe die Gabe des Hellsehens und er könne mit traumwandlerischer Sicherheit jeweils den Übergang nehmen, der schließlich in einen Endzustand führt (so es diesen gibt) oder es gleich aufgibt (wenn nicht). Manchmal konstruiert man für so etwas auch ein so genanntes Orakel, das der NDEA in Ermangelung eigener transzendenter Fähigkeiten zu Rate ziehen kann.

Diese Orakel gibt es natürlich nicht wirklich, und so muss man, wenn man einen NDEA simuliert, eben doch alle Möglichkeiten durchprobieren. Das ist unter Umständen viel verlangt – es gibt potenziell eine gewaltige Menge möglicher Zustandsfolgen. In realen Computern ist die Auswertung von NDEAs daher nicht ganz einfach (mit Quantencomputern könnte sich das ändern, für sie sind NDEAs quasi wie geschaffen, aber wir haben noch keine wirklich brauchbaren Quantencomputer).

Welche Sprache akzeptieren nun NDEAs? Das lässt sich recht analog zur Entwicklung bei DEAs beantworten, also durch Bildung einer erweiterten Übergangsfunktion δ^*, nur, dass wir dieses Mal damit rechnen müssen, dass wir nicht einen, sondern mehrere Zustände zurückbekommen.

Definieren wir also

Mit anderen Worten berechnen wir die Menge der Zustände in denen sich der NDEA nach dem Lesen von wx befinden kann dadurch, dass wir erst alle Zustände berechnen in denen er nach dem Lesen von w stehen kann und dann für jeden dieser Zustände sehen, in welche er beim Lesen von x von dort aus gehen kann. Die Ergebnisse δ(Z,x) sind Mengen (wir haben ja einen NDEA), und die vereinigen wir, fertig. Wir definieren dann

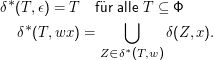
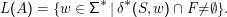
Verglichen mit der entsprechenden Definition für DEAs hat sich nur die Entscheidung geändert, ob wir akzeptieren wollen oder nicht – haben wir damals geprüft, ob der Zustand am Ende der Eingabe in der Menge der Endzustände ist, müssen wir jetzt sehen, ob einer der potenziell vielen Zustände, in denen wir uns am Ende der Eingabe befinden können, ein Endzustand ist – ob also die Menge der Endzustände F mit der Menge δ^*(S,w) der möglichen Zustände nach dem Lesen von w mindestens ein gemeinsames Element hat.

Erstaunlicherweise gilt der folgende Satz von Rabin und Scott:

NDEAs und DEAs sind äquivalent.

Beweisidee: Φ_DEA =℘(Φ_NDEA)

Formal wollen wir beweisen, dass es zu jeder durch einen NDEA A= ⟨Φ,Σ,δ,S,F⟩ (Vorsicht: S ist hier eine Menge!) akzeptierten Sprache L auch einen DEA A‘ gibt, der gerade L akzeptiert. Dieser DEA wird nach Beweisidee die folgende Form haben:

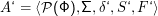
Was muss nun δ‘ sein? Wir wollen unseren NDEA durch den DEA simulieren, indem wir uns nicht gleich entscheiden, in welchen Zustand wir übergehen, sondern erstmal in mehreren NDEA-Zuständen gleichzeitig sind – also in einer Teilmenge von Φ. Deswegen wollen wir aus einem DEA-Zustand Z‘ einfach in den DEA-Zustand übergehen, der aus allen NDEA-Zuständen besteht, die wir von allen NDEA-Zuständen φ in Z’ unter Lesen des augenblicklichen Zeichens x erreichen können, also

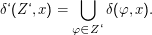
Die Teilmenge von Φ, in der sich der NDEA am Anfang befinden kann, ist gerade S, also muss der Startzustand S‘ = S sein.

Ein NDEA akzeptiert, wenn einer der der möglichen Zustände am Ende der Eingabe in der Menge der Endzustände enthalten ist; Endzustände des DEA sind mithin alle Zustände, die mindestens ein Element aus F enthalten.

Damit haben wir den DEA konstruiert:

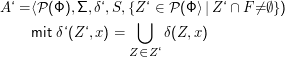
Prüfen wir, ob L(A) = L(A‘) gilt, wir also bei unserer Konstruktion keinen Fehler gemacht haben. Sei zunächst w= x₁…x_n ∈L(A). Wir müssen dazu zeigen, dass die Zustandsfolge, die der DEA beim Lesen von w durchläuft, schließlich in einem Endzustand des DEA endet.

Was ist diese Zustandsfolge? Nun, interessanterweise sind die Z_i = δ^*(S,x₁…x_i-1) (wir vereinbaren x₁…x₀ = ϵ, um die Schreibweise zu vereinfachen), also die Werte von δ^* nach dem Lesen der ersten i- 1 Zeichen des Wortes, gerade DEA-Zustände (nämlich Teilmengen von Φ). Könnte es nicht sein, dass Z₁,…,Z_n+1 die gesuchte DEA-Zustandsfolge ist?

Dem ist tatsächlich so; um das zu sehen, reicht etwas Indexzauberei:

(prüft das mit den Formeln für δ‘, δ^* und Z_i!)

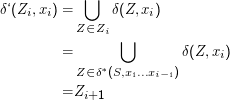
Um sicher zu sein, dass DEA und NDEA auch an der gleichen Stelle loslaufen, vergewissern wir uns noch, dass in der Tat

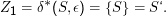
Schließlich müssen wir noch sehen, dass der DEA das Wort auch akzeptiert. Das tut er aber, weil

– die Ungleichung gilt, weil w∈L(A) ist, mit dem Gleichheitszeichen gilt dann aber nach Definition Z_n+1 ∈F‘, also w∈L(A‘), und das war es, was wir wissen wollten.

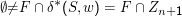
Als Beispiel für die Wandlung eines NDEA in einen DEA betrachten wir den Vielleicht-Automaten. Dessen Übergangsfunktion ist

die Potenzmenge der Zustandsmenge

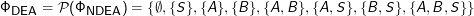
Der Startzustand ist einfach: S‘ = {S}, weil auch der NDEA nur einen Startzustand hat.

Zulässige Endzustände des DEA sind alle Mengen, die Endzustände des NDEA enthalten. Endzustand des NDEA ist wieder nur S, wir haben also insgesamt vier DEA-Endzustände.

Die Übergangsfunktion rechnen wir nur für die wirklich interessanten Fälle aus, also die Zustände, die auch wirklich erreicht werden. Das ist zunächst

Beachtet, wie sich δ‘ aus dem Wert von δ ergibt. δ‘({S},ja) ergibt sich auf diese Weise zur leeren Menge, und analog zum nein-Fall sparen wir uns das Hinschreiben.

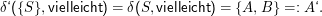
Wir haben jetzt aber einen neuen Zustand A‘ = {A,B} und müssen δ‘ für ihn ausrechnen:

Alle anderen Zustände sind vom Startsymbol aus nicht erreichbar und daher uninteressant; nicht erreichbare Zustände können wir natürlich auch aus der Zustandsmenge streichen, so dass wir insgesamt zwei Zustände mit insgesamt drei Übergängen haben.

In diesem speziellen Fall hat uns dieses Verfahren also einen kleineren Automaten geliefert als den oben von mir vorgeschlagenen. Das ist aber sehr untypisch. In der Regel bekommt man aus so einer Umwandlung gewaltige DEAs heraus – was auch nicht so überraschend ist, ist doch hier eine Potenzmenge im Spiel. Man kann die DEAs auch etwas besser konstruieren oder aber einige bekannte Verfahren einsetzen, um die DEAs automatisch zu verkleinern.

Es ist aber keineswegs sicher, dass das viel bringt. Die Sprache aller Wörter aus {0,1}^* mit einer 0 an der k-letzten Stelle ist z.B. mit einem NDEA mit k+ 1 Zuständen zu erkennen und damit regulär. Für k= 3 sieht so ein NDEA etwa so aus:

Ein DEA, der diese Sprache akzeptiert, muss aber mindestens 2^k Zustände haben (der Beweis dafür ist nicht schwierig und findet sich z.B. bei Schöning) – und das macht schon bei relativ moderaten k von vielleicht 30 dieses Problem für DEAs unzugänglich.

In gewisser Weise könnte man NDEAs also als “Konstruktionshilfen für DEAs” bezeichnen.