19. Automaten I

Wir können jetzt reguläre Sprachen entweder durch eine einseitig linearen Grammatik oder aber durch Hinschreiben eines regulären Ausdrucks definieren. Diese Formalismen bieten Methoden, mit deren Hilfe man sämtliche Elemente einer Sprache L aufzählen kann. Zur Entscheidung, ob ein Wort 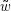in einer Sprache ist oder nicht, ist es jedoch höchst mühsam, einfach ein Wort nach dem anderen zu erzeugen und darauf zu warten, dass irgendwann 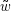vorkommt – zumal auf diese Weise ohne weitere Maßnahmen eine Entscheidung, dass 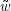nicht in L ist, für den Regelfall unendlicher Sprachen nicht möglich ist, denn wir können eben nicht ausschließen, dass gerade das nächste Wort in unserer Aufzählung 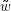ist.

Deshalb wollen wir jetzt in gewisser Weise den umgekehrten Weg gehen: Wir möchten ein Verfahren, das möglichst einfach entscheidet, ob ein Wort in einer irgendwie definierten Sprache ist oder nicht (“das Wortproblem löst”). Solche Verfahren verwenden gemeinhin Automaten, im Fall der regulären Sprachen die deterministischen endlichen Automaten.

Ein deterministischer endlicher Automat (DEA) ist ein Tupel ⟨Φ,Σ,δ,S,F⟩ aus

1. Einem Zustandsalphabet Φ
2. Einem zu Φ disjunkten Eingabealphabet Σ
3. Einer Übergangsfunktion δ:Φ ×Σ →Φ
4. Einem Startzustand S∈Φ
5. Einer Menge F⊂Φ von Endzuständen

Ein Automat befindet sich am Anfang im Startzustand S und liest das erste Zeichen x₁ ∈Σ eines Eingabewortes w. Er geht daraufhin in den Zustand T= δ(S,x₁) und liest x₂, um damit nach δ(T,x₂) zu gehen usf. Ist er in einem Endzustand (einem Zustand aus F), wenn die Eingabe abgearbeitet ist, ist w akzeptiert, sonst nicht.

Der folgende DEA akzeptiert beispielsweise einfache HTML-Tags (sie folgen dem regulären Ausdruck </?[a-z]+> (in Unix-Schreibweise) oder

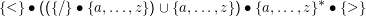
Man stellt DEAs im Allgemeinen als Graphen der Übergangsfunktion δ dar. Leider ist δ aber kein Graph (dazu müsste er eine Relation zwischen Φ und Φ, also eine Abbildung Φ →Φ sein). Die Komplikation mit dem Σ lösen wir durch Ausweichen auf markierte Graphen (labeled graphs). Dabei malen wir an jede Kante < φ₁,φ₂ >, φ_1,2 ∈Φ das Zeichen x, das im in δ enthaltenen Tupel << φ₁,x >,φ₂ > steht. Das klingt kompliziert, ist aber ganz einfach:

Endzustände zeichnet man konventionell als doppelte Kreise, den Anfangszustand markiert man manchmal durch einen kleinen Pfeil “aus dem Unendlichen”.

Sehen wir, ob der HTML-Tag <br> von diesem Automaten erkannt wird. Dazu laufen wir den Automaten einfach durch und schreiben über jeden Übergang das Zeichen, was wir für diesen Übergang gelesen haben:

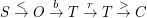
C ist ein Endzustand, deshalb ist das ein korrekter HTML-Tag.

Demgegenüber wollen wir </g< zurückweisen. Konventionell bleibt ein Automat einfach stehen, wenn ein Zeichen gelesen wird, für das es keinen Übergang gibt (alternativ könnte man einen “Fehlerzustand” E einführen, und δ durch << φ,x >,E > ergänzen, wenn es für alle ψ∈Φ keinen Übergang << φ,x >,ψ >∈δ gibt). Dann sieht unser Weg durch den Automaten so aus:

Wir sind nicht in einem Endzustand angekommen, das Wort wird nicht akzeptiert.

Analog zur Verallgemeinerung der direkten Ableitung → zur Ableitbarkeit * → bei Grammatiken können wir für DEAs eine Übergangsfunktion δ^* : Φ ×Σ^*→Φ für ganze Wörter definieren, etwa durch

• δ^*(T,ϵ) = T und
• δ^* (T, wx) = δδ^*(T,w),x.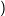

Wieder ist das mehr eine formale Geschichte – für nichttriviale Grammatiken ist δ^* ein unendlicher Graph, der in der Praxis nicht ganz berechnet werden kann. Die Definition erlaubt uns aber, einen weiteren Begriff zu fassen.

Analog zur von einer Grammatik erzeugten Sprache ist die von einem Automaten A= ⟨Φ,Σ,δ,S,F⟩akzeptierte Sprache L(A) = {w∈Σ^*|δ^*(S,w) ∈F}.

Das ist einfach die Menge der Wörter, die auf einen Endzustand führen.