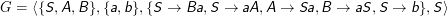18. Einseitig Lineare Grammatiken

Ich hatte oben verkündet, dass wir Sprachen durch Grammatiken definieren wollten – und nun haben wir stattdessen einen ganz anderen Formalismus eingeführt, nämlich reguläre Ausdrücke. Auch diese beschreiben, wie die Wörter einer Sprache aussehen sollen. Wenn der Grammatikformalismus auch nur irgendetwas taugt, dann sollte er eigentlich auch “können”, was die regulären Ausdrücke können. Das ist in der Tat so.

Eine Grammatik G= ⟨Φ,Σ,R,S⟩ heißt rechtslinear (linkslinear), wenn alle Regeln eine der beiden Formen

• A→w oder
• A→wB (A→Bw)

haben, wobei A,B∈Φ und w∈Σ^*(Chomsky-3-Grammatik).

Lemma: Jede reguläre Sprache wird durch eine rechtslineare Grammatik erzeugt.

Wir wollen die beiden Behauptungen des Satzes getrennt beweisen. Dabei beschränken wir uns auf den rechtslinearen Fall, der linkslineare wäre ähnlich zu behandeln.

Beweis: Wir geben für alle Operatoren in einem regulären Ausdrucks rechtslineare Grammatiken.

1. ∅: G_∅ = ⟨{S},Σ,{S→S},S⟩.
2. {a_i }: G_ai = ⟨{S},Σ,{S→a_i},S⟩.
3. L(G₁ ) ∪L(G₂): G_∪ = ⟨Φ₁ ∪Φ₂,Σ₁ ∪Σ₂,R₁ ∪R₂ ∪{S→S₁,S→S₂},S⟩.Dabei sollen G₁ = ⟨Φ₁,Σ₁,R₁,S₁⟩ und G₂ = ⟨Φ₂,Σ₂,R₂,S₂⟩ rechtslineare Grammatiken sein, wobei Φ₁ ∩Φ₂ = ∅ (das ist durch Umbenennen immer möglich).
4. L(G₁ ) ∙L(G₂): G_∙ = ⟨Φ₁ ∪Φ₂,Σ₁ ∪Σ₂,{A→wS₂ |A→w∈R₁}∪{A→wB|A→wB∈R₁}∪R₂,S₁⟩. Hier hätte man versucht sein können, einfach wie im Fall eben eine Regel S→S₁S₂ zur Vereinigung der beiden Regelmengen hinzuzufügen. Das würde auch in der Tat die Verkettung erzeugen, nur wäre die resultierende Regelmenge nicht mehr rechtslinear. Das würde unseren Beweis kaputt machen, und deshalb machen wir den etwas aufwändigeren Trick, einfach alle Regeln, die ein Wort aus L(G₁) vollenden würden (die also die Form A→w haben) so umzuschreiben, dass ein Wort aus L(G₂) folgt (wir hängen also S₂ an).
5. L(G)^*: G_* = ⟨Φ,Σ,{A→wS|A→w∈R}∪{A→wB|A→wB∈R}∪{S→ϵ},S⟩.

Lemma: Jede durch eine rechtslineare Grammatik erzeugte Sprache wird auch durch einen regulären Ausdruck beschrieben.

Der folgende Beweis ist konstruktiv, d.h. er beweist nicht einfach nur, dass es einen regulären Ausdruck zu einer einseitig linearen Grammatik gibt, sondern gibt sogar ein Verfahren an, wie er zu konstruieren sei. Wir wollen den Beweis eher informell und wortreich angehen, quasi zur Eingewöhnung.

Wir haben eine rechtslineare Grammatik G= ⟨Φ,Σ,R,A₁⟩. Φ soll zwecks einfacher Notation aus A₁, A₂,…, A_n bestehen (das ist durch Umbenennen immer zu garantieren). Σ ist beliebig, R darf nur rechtslineare Regeln enthalten.

Der Hit an den rechtslinearen Grammatiken ist, dass die Art, wie sie ihre Wörter erzeugen, recht einfach ist: Sie wachsen immer nur nach hinten. Vor jeder Ableitung steht immer ein Nichtterminalsymbol ganz am Ende des augenblicklichen Wortes. Nach dieser Ableitung steht dann entweder wieder ein Nichtterminalsymbol am Ende, oder aber ein Terminalsymbol. Im zweiten Fall ist die Ableitung zu Ende, weil wir ohne Nichtterminalsymbol nicht weiter ableiten können.

Damit kommt der letzten Ableitung eine besondere Bedeutung zu, und wir wollen sehen, was dabei passieren kann.

Wir definieren dazu die Mengen N(j) als die Nichtterminale, die jeweils von A_j aus direkt erzeugt werden, formal

Damit wir nicht wahnsinnig werden, schreiben Formeln dieser Art ab jetzt als N(j) = {w|A_j →w}– die Notation ist kürzer und ähnlich klar.

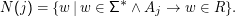
Diese Mengen sagen uns gerade, was am Ende eines Wortes stehen kann. Wenn A_j überhaupt jemals in Ableitungen vorkommt, muss es auch Wörter geben, in denen ein Element von N(j) am Ende steht, denn auch das A_j kann in rechtslinearen Grammatiken immer nur am Ende eines Wortes (aus Γ^* – in Wörtern der erzeugten Sprache hat es als Nichtterminalsystem natürlich nichts verloren) auftreten. Wenn es also überhaupt einen regulären Ausdruck gibt, der L(G) beschreibt, muss er die Form … ∙N(j) haben.

Leider ist das, was an die Stelle der drei Punkte kommt, unübersichtlich. Es ist naheliegend, das Problem aufzuspalten (“divide et impera”), aber wie? Nun, angenommen, wir dürften nur zwei Ableitungsschritte machen. Dann müssten wir im ersten Schritt irgendeine Regel der Art A₁ →w‘A_j anwenden, im zweiten Schritt käme der eben skizzierte “Abschluss” dran.

Was sind die möglichen w‘, wenn wir über A_j zum Ende kommen? Das muss einfach die Menge S(j) = {w‘|A₁ →w‘A_j} sein. Dann wäre unsere Sprache ⋃ _j=1…nS(j) ∙N(j), die Menge aller Wörter, die durch Verkettung von Kram, der von A₁ kommend vor A_j stehen kann, verkettet mit allem Kram, der aus A_j werden kann, ohne dass ein weiteres Nichtterminal auftaucht, und den Kram dann wieder für alle A_j vereinigt.

Halt – da ist noch Fehler: Es kann ja auch passieren, dass es Regeln A₁ →w gibt, und die w, die dabei auftauchen, wären noch nicht erfasst. Das ist schnell repariert:

Damit hätten wir den regulären Ausdruck, weil sowohl S(j) als auch N(j) endlich und damit regulär sind.

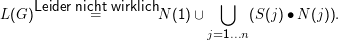
Leider ist es nicht so einfach, weil es eben mehr als zwei Ableitungsschritte geben kann. Aber die Idee trägt ja vielleicht: Definieren wir mal die Menge aller w∈Σ^*, die vor der letzten Ableitung vor einem A_j stehen können, 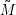(j). Mit dieser Schreibweise sieht der resultierende Ausdruck immer noch ziemlich regulär aus:

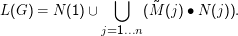
In Wirklichkeit sind wir aber nicht viel weiter, denn ein regulärer Ausdruck ist das nur dann, wenn die 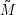(j) wirklich regulär sind. Um das zu zeigen, braucht es einen Trick, der in der Mathematik populär ist – wir sehen uns etwas allgemeinere Gebilde an, nämlich die Mengen der Wörter in w∈Σ^*, die bei einer Ableitung A_i * →wA _j auftreten können,

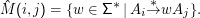
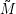Speziell ist (j) = M(1,j), wenn wir also zeigen können, dass die 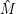(i,j) regulär sind, sind wir auch schon fertig.

Leider ist auch den 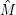die Regularität noch nicht anzusehen. Hier kommt der eigentliche “kreative Akt” des Beweises, wir müssen nämlich besonders geschickt aufteilen. Dazu definieren wir Mengen M(i,j,k), die Teilmengen von 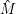(i,j), bei denen während der Ableitung nur die ersten k Nichtterminalsymbole A₁,…,A_k verwendet werden. So seltsam diese Mengen zunächst auch sind, es ist klar, dass

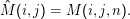
Dieser Umweg lohnt sich, weil man die M(i,j,k) relativ leicht auf “einfachere” M(i,j‘,k‘) zurückführen kann. Mit einem Induktionsbeweis kann man dann zeigen, dass sie selbst und damit auch die 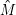(i,j) als endliche Vereinigung von M(i,j,k) regulär sind. Mit ihnen sind auch alle 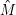(i,j) regulär, also auch alle 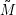(j) und damit schließlich nach der Formel oben auch L(G) selbst.

Diesen entscheidenden Beweisschritt lagern wir in einen Hilfssatz aus. In der Mathematik sagt man statt Hilfssatz gerne auch Lemma – wir schließen uns dem an.

Lemma: Die Mengen M(i,j,k) sind regulär.

Beweis durch Induktion.

Induktionsanfang: k= 0. M(i,j,0) ist die Menge der w, die beim Übergang von A_i auf A_j unter Verwendung keiner anderen Nichtterminale (A_i und A_j eingeschlossen) entstehen können. Das ist aber gerade die Menge

Da es nur endlich viele Regeln gibt, ist das eine endliche Menge und deshalb regulär.

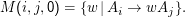
Induktionssannahme: Sei M(i,j,k) für k≥ 0 regulär.

Induktionsschluss: Von k auf k+ 1. Wir müssen also aus der Annahme, dass M(i,j,k) regulär ist, auf die Regularität von M(i,j,k+ 1) schließen.

Was steht in M(i,j,k+ 1)? Nun, auf jeden Fall alles, was schon in M(i,j,k) drin ist. Die Wörter, die dazu kommen, verwenden irgendwo das Nichtterminal A_k+1. Auf dem Weg zu dieser Verwendung wird ein Element aus M(i, k+ 1,k) beigetragen – wir laufen bei A_i los, verwenden die ersten k Nichtterminale und kommen dann schließlich bei A_k+1 raus. Von dort müssen wir dann wieder zu A_j kommen – dabei wird dann ein Element von M(k+ 1,j,k) beigetragen. Die Überlegung hat noch eine Lücke: Wir dürfen mehrmals bei A_k+1 vorbeischauen, wir dürfen das sogar machen, so oft wir wollen. Bei jedem dieser Wege laufen wir mit A_k+1 los und kommen wieder bei A_k+1 raus, bekommen also Elemente aus M(k+ 1,k+ 1,k) zu unserem Wort dazu. Zusammen heißt das:

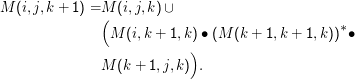
Nach der Induktionsannahme sind aber M(i,j,k) alle regulär. In diesem Ausdruck werden also reguläre Mengen verkettet, vereinigt und versternt – es ist also ein regulärer Ausdruck, und das zeigt die die Behauptung.

Zusammengefasst gilt also:

Wenn G= ⟨{A₁,…,A_n},Σ,R,A₁⟩ rechtslinear ist, gilt

wobei N und M reguläre Mengen sind.

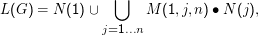
Insgesamt gilt:

Satz: Reguläre Ausdrücke und einseitig lineare Grammatiken sind äquivalente Formalismen zur Beschreibung von Sprache.

Mit “äquivalent” ist dabei gemeint, was die beiden “großen” Lemmata sagen: Zu jedem regulären Ausdruck finde ich eine rechtslineare Grammatik und zu jeder rechtslinearen Grammatik finde ich einen regulären Ausdruck, die jeweils identische Sprachen beschreiben.

Nachgewiesen haben wir das nur für rechtslineare Grammatiken, aber die Beweise für linkslineare Grammatiken funktionieren analog. Linkslineare Grammatiken sind allerdings meistens langweiliger.

Beachtet nochmal, dass ihr nicht links- und rechtslineare Regeln in einer Regelmenge mischen dürft und erwarten könnt, dass das Ergebnis immer noch regulär ist. Die Grammatik

beispielsweise erzeugt die Sprache {aⁱbaⁱ}, die, wie wir noch zeigen werden, nicht regulär ist.