(1)
Im Satzsystem TEX folgen Kontrollsequenzen ohne weitere Einstellungen ungefähr folgendem regulären Ausdruck:
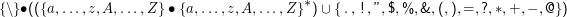
Findet Invarianten der von diesem regulären Ausdruck erzeugten Sprache.
Ein regulärer Ausdruck über einem Alphabet Σ ist definiert durch
Vorsicht: Die Ausdrücke hier sind sozusagen “verzögert”: Die Mengenoperationen werden nicht ausgeführt, sondern hingeschrieben. Werden sie ausgeführt, erhält man:
Eine reguläre Sprache ist eine formale Sprache, die durch einen regulären Ausdruck beschrieben werden kann.
Beispiele: Sei Σ = {a,b,c}. Reguläre Sprachen über Σ sind beispielsweise ((({a,b}∙{b}) ∪{c,a}*) ∙{c}) oder Σ* .
Zählen wir ein paar Elemente der ersten Sprache auf. Wir haben “ganz außen” eine Verkettung mit {c} als zweiten Operanden. Der erste Operand dieser Verkettung ist kompliziert, aber wir können ihn nach und nach ansehen. Er besteht aus einer Vereinigung, deren erster Operand zur fertigen Sprache (d.h. nach der Verkettung mit dem {c})
beiträgt. Der zweite Operand der Vereinigung ist unendlich, wir können mit der Aufzählung der fertigen Wörter also nur anfangen:
Das sind alle Wörter der Sprache, die aus drei Zeichen aufgebaut sind. Man sieht, dass Sprachen selbst im einfachsten Fall (das sind die regulären Sprachen) schon sehr unübersichtlich werden können.
Deshalb ist es wichtig, Invarianten zu erkennen, Eigenschaften, die allen Wörtern gemein sind. Hier ist das beispielsweise, dass am Ende jeden Wortes immer ein c steht – das ist in diesem Fall bereits am regulären Ausdruck zu erkennen (die letzte Verkettung). Invarianten können aber auch etwas komplizierter sein – im Beispiel wäre eine weitere Invariante, dass alle Wörter, die ein b enthalten, mit bc enden (überzeugt euch durch Inspektion des Ausdrucks von dieser Eigenschaft).
Reguläre Ausdrücke werden z.B. von grep, emacs, vi, perl, python und vielen anderen verstanden. Schreibweise dort: Sternbildung durch *, Mengenbildung durch [] (für einzelne Zeichen) oder (.|...), Vereinigung durch |, Verkettung durch hinereinanderschreiben. Die beiden regulären Ausdrücke oben würden damit etwa ([ab]b|[ac]*)c bzw. [abc]* entsprechen.
Reguläre Ausdrücke können z.B. für Zahlen angegeben werden. Sie können aber nicht Elemente gegeneinander aufzählen: Es gibt keinen regulären Ausdruck, der die Balanciertheit von Klammern feststellen kann (das werden wir später beweisen).
Klassisch: {aibai|i∈ℕ} ist keine reguläre Sprache.
Ihr solltet euch wenigstens an den rötlich unterlegten Aufgaben versuchen
(1)
Im Satzsystem TEX folgen Kontrollsequenzen ohne weitere Einstellungen ungefähr folgendem regulären Ausdruck:
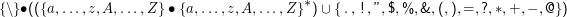
Findet Invarianten der von diesem regulären Ausdruck erzeugten Sprache.
(2)
Bildet den Partizip Perfekt von einer Handvoll deutscher Verben. Findet ihr in der dadurch definierten Sprache Invarianten?
Geht auf eine nicht allzu öde Webseite und lasst euch von eurem Browser die darin eingebetteten Links anzeigen (bei einem englischsprachigen Firefox geht das z.B. durch Tools/Page Info, Tab “Links”). Findet ihr in der durch diese Links (Feld “Address”) definierten Sprache Invarianten?