Eine Ableitung (auch Parse genannt) in einer Grammatik G= ⟨Φ,Σ,R,S⟩ ist eine Folge von Wörtern wi aus (Φ ∪Σ)*, so dass wi →wi+1 und w1 = S.
Gegeben sei

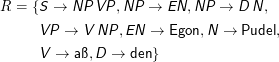
Eine Ableitung des Wortes “Egon aß den Pudel” ist
| S | → | NP VP | → | EN VP | → |
| EgonVP | → | Egon V NP | → | Egon aß NP | → |
| Egon aß D N | → | Egon aß den N | → | Egon aß den Pudel |
In der Regel gibt es zu einem Wort mehrere Ableitungen. Eine weitere Ableitung für “Egon aß den Pudel” ist:
| S | → | NP VP | → | NP V NP | → |
| NP V D N | → | NP V D Pudel | → | NP V den Pudel | → |
| NP aß den Pudel | → | EN aß den Pudel | → | Egon aß den Pudel |
Beide Ableitungen führen auf den gleichen Baum:
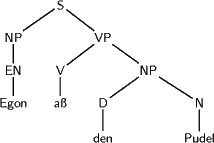
Wie entsteht dieser Baum aus den Ableitungen? Nun, jeder innere Knoten (d.h. Knoten, der kein Blatt ist) k repräsentiert eine Regelanwendung, wobei die Wurzel des Unterbaums unterhalb von k der linken Seite der Regel entspricht, die direkten Nachfolger den Symbolen auf der rechten Seite der Regel. Um also den Baum zu malen, muss man eigentlich nur bei jedem Ableitungsschritt die angewandte Regel identifizieren und an der passenden Stelle die Symbole auf der rechten Seite dieser Regel als neue Blätter hinmalen; die passende Stelle wiederum ist das Nichtterminalsymbol, das ersetzt wurde.
Dabei kann es vorkommen, dass zwei Mal das gleiche Nichtterminalsymbol als Blatt im augenblicklichen Parsebaum vorkommt – der dritte Schritt in der zweiten Ableitung oben ist ein Beispiel dafür, wir haben zwei Mal NP. Es ist dann natürlich entscheidend wichtig, dass man die richtige NP zum Ersetzen wählt.
Bäume dieser Art können natürlich nur gebildet werden, wenn auf der linken Seite aller Regeln nur ein Nichtterminalsymbol steht – andernfalls wäre jedes Symbol auf einer linken Seite Vorgänger jeden Symbols auf der rechten Seite und das Ergebnis wäre kein Baum mehr.