15. Grammatiken und Ableitungen

Sprachen können wir im Prinzip wie Mengen definieren – sie sind ja nur Mengen. Einfach alle Wörter aufzählen ist aber im Regelfall unmöglich, weil “interessante” Sprachen typischerweise abzählbar unendlich viele Wörter enthalten.

Da wäre die set comprehension schon viel netter, und eigentlich würde auch die rekursive Definition taugen, nur: wie konkret soll die Definition aussehen, wie können wir das Aussehen der Wörter beschreiben? “Ein a am Anfang, und dann kommt entweder ein o oder ein c, es kann aber auch sein, dass das Wort mit b anfängt, und dann…” Nein – wir brauchen einen Formalismus für diese Beschreibung, und ein Industriestandard dafür sind Grammatiken, die sozusagen vorschreiben, wie man Wörter nach und nach aufbaut.

Eine Grammatik ist ein Tupel G= ⟨Φ,Σ,R,S⟩ aus

• einem Alphabet Φ von Nichtterminalsymbolen – das sind Symbole, die am Schluss in den Wörtern der Sprache nicht mehr auftauchen sollen, ein bisschen so, wie der Quelltext eines Programms in seiner Ausgabe nichts verloren hat
• einem Alphabet Σ von Terminalsymbolen, wobei Σ ∩Φ = ∅ – das sind die Symbole, die am Schluss in den fertigen Wörtern der Sprache stehen werden. Gelegentlich schreiben wir Γ := Σ ∪Φ.
• einer Menge von Regeln R⊂Γ^*×Γ^* = {< α_i,β_i >}, wobei α_i∉Σ^*.
• einem Startsymbol S∈Φ.

Insbesondere ist α_i≠ϵ. Also: Regeln ersetzen nie ausschließlich Folgen von Terminalsymbolen (daher deren Name) und ersetzen nie das leere Wort.

Diese Grammatik heißt auch Typ 0- oder allgemeine Regelgrammatik. Andere Grammatiktypen gehen durch weitere Forderungen an die Regeln hervor.

Den Grammatikbegriff hatten wir eingeführt, um Sprachen beschreiben zu können. Im Groben würden wir jetzt ganz gerne sagen: Die Sprache L besteht aus den Wörtern, die ich durch wiederholte Anwendung der Regeln aus dem Startsymbol erzeugen, wir werden sagen: ableiten kann. Das müssen wir jetzt etwas vornehmer formulieren.

Seien u,v∈Γ^*. Dann heißt v aus u direkt ableitbar, wenn u= u₁wu₂ und v= u₁zu₂ und < w,z >∈R.

In einer Grammatik

gilt abSba →abaSaba und bbbS →bbbb, aber nicht S →ba oder abS →aSa. Im Zweifel kann man die Wörter rechts und links nach u₁, u₂, w und z aufteilen und dann sehen, ob die Definition von direkter Ableitbarkeit erfüllt ist.

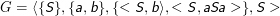
Gut – wir haben jetzt eine Relation definiert, nämlich die der direkten Ableitbarkeit. Zur Übung kann man mal sehen, welche Eigenschaften sie hat: Sie ist nicht transitiv (es gilt mit der Grammatik oben zwar S →aSa und aSa →aba, aber nicht S →aba), sie ist nicht symmetrisch und auch nicht reflexiv (es gilt also insbesondere nicht S →S).

Sie reicht aber eigentlich schon für eine rekursive Definition der Sprache L(G), die aus allen Wörtern besteht, die die Grammatik G erzeugt. Probieren wir es erstmal mit einer Sprache L‘:

1. S∈L‘
2. Wenn w∈L‘ und w→w‘, dann ist auch w‘ ∈L‘.

Das Problem an dieser Definition ist, dass in L‘ allerlei Wörter wie aaSaa stehen – wir hatten aber oben verlangt, dass in den fertigen Wörtern nur noch Terminale, aber keine Nichtterminale stehen sollten. Das Problem ist lösbar, wir können einfach sagen, dass L(G) = {w|w∈L‘ ∧w∈Σ^*} sein soll.

Das ist keine schlechte Definition, aber die Leute verstecken die Rekursion lieber etwas. Dafür brauchen wir nun die transitive Hülle – wir hatten ja oben beklagt, dass nicht S →aba gilt, also die direkte Ableitbarkeit nicht transitiv ist. In der transititiven Hülle von → ist aber das Paar <S,aba > durchaus enthalten. Also definieren wir:

Seien u,v∈Γ^*. Dann heißt v aus u ableitbar (in Zeichen: u * →v), wenn u= u ₁wu₂ und v= u₁zu₂ und < w, z >∈P⁺, wo P die durch die direkte Ableitbarkeit definierte Relation ist.

Damit können wir die erzeugte Sprache ganz ohne Rekursion definieren (denn die Rekursion haben wir schon bei der Definition der transitiven Hülle erledigt).

Die erzeugte Sprache

L(G) = {w∈Σ^*|S * →w} ist die von einer Grammatik G= ⟨Φ,Σ,R,S⟩erzeugte Sprache (umgekehrt gibt es keine (eindeutige) von einer Sprache erzeugte Grammatik).

Beispiel: Sei

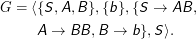
Dann ist

(die drei Punkte deuten an, dass die Relation natürlich noch beliebig viele weitere Elemente hat – rechnet ein paar weitere aus –, die aber zum Glück keine Relevanz für die Bestimmung der erzeugten Sprache haben).

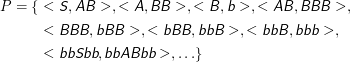
Damit ist

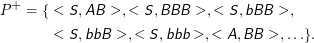
Wieder hat diese Relation natürlich beliebig viele weitere Elemente. Allerdings ist bbb das einzige Element von Σ^*, das als zweites Element in einem Tupel mit S auftaucht, und damit hätten wir schon die erzeugte Sprache: L(G) = {bbb}.

Natürlich rechnet niemand wirklich auf diese Weise Sprachen aus. Aber das ist die Definition, und irgendwelche anderen Verfahren müssen die Ergebnisse dieses eingestandenermaßen umständlichen Verfahrens beweisbar reproduzieren.

Nebenbei bemerkt interessiert man sich in der Regel eher dafür, wie ein Wort erzeugt wurde. Sprachen wortweise Aufzählen ist eine eher ungewöhnliche Beschäftigung.