14. Vokabeln

Alphabet: Eine nicht-leere Menge von Zeichen. Hier betrachten wir nur endliche Alphabete. Σ bezeichnet im Folgenden immer ein Alphabet. Was wir dabei als Zeichen ansehen, ist eigentlich relativ egal. Wir werden der Einfachheit halber meist lateinische Groß- und Kleinbuchstaben nehmen, manchmal auch ASCII-Zeichen – aber wie schongesagt wären “Wörter” der Natursprache genauso möglich wie Morphe, Formelzeichen oder Tokens von Programmiersprachen.

Wort: Eine Folge (x_i)_i∈{1…n} von Zeichen x_i ∈Σ. Es muss betont werden, dass sich dies deutlich von fast allen Definitionen von “Wort” in der Linguistik unterscheidet, selbst wenn man als Alphabet tatsächlich ein Alphabet einer Natursprache verwendet. Allerdings wird auch und gerade Morphologie gern mit den hier besprochenen Methoden betrieben, und dann ist ein Wort auch ziemlich gut ein Wort, während ein Zeichen vielleicht ein Morph oder auch ein Buchstabe ist.

Konkatenation, auch Verkettung: Wenn w= (w_i)_i∈{1…n} und v= (v_i)_i∈{1…m} mit w_i,v_i ∈Σ, dann die Verkettung u= w∙v (meistens lassen wir das ∙ weg und schreiben einfach wv) definiert als u= (u_i)_{i∈{1…n+m}} mit

Das ist MathematikerInnensprache für “Wir schreiben die Zeichen halt hintereinander.” Wie so oft, verbirgt sich hinter komplizierten Zeichen, die einfach die Operation genau und unzweideutig definieren, ein ganz einfacher Sachverhalt. Wenn w= abc und v= cba, dann ist eben w∙v= abccba. Das Ganze kann man auch für Mengen machen: Wenn M₁ , M₂ ⊂Σ^*, dann ist

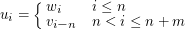
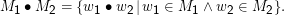
leeres Wort: Das aus null Zeichen bestehende Wort ϵ= (ϵ_i)_i=0..0. Es ist für alle Wörter w∙ϵ= w. ϵ spielt also für die Verkettung in etwa die Rolle des Neutralen Elements, ganz wie die Null bei der Addition. N.B. ∅≠{ϵ}.

Länge eines Worts: Die Zahl der Zeichen in einem Wort w, in Zeichen |w|. Eine elegante rekursive Definition ist: (a) |ϵ|= 0, (b) |aw|= |wa|= 1 + |w| für ein Wort w∈Σ^* und a∈Σ. Generell ist die Idee rekursiver (oder induktiver) Definitionen, eine Eigenschaft für etwas “Größeres” durch das Nächstkleinere zu bestimmen. Hier wird die Länge eines Wortes mit einem angehängten Zeichen durch die Länge des nackten Wortes bestimmt.

Sternbildung: Die Menge aller Worte über einem Alphabet Σ wird mit Σ^* bezeichnet. Eine rekursive Definition ist: (a) ϵ∈Σ^*, (b) w∈Σ^*∧a∈Σ ⇒aw∈Σ^*. Für ein endliches Alphabet ist Σ^* abzählbar unendlich. Dies kann man zeigen durch die Angabe einer Bijektion zu den natürlichen Zahlen. Eine injektive Abbildung in die natürlichen Zahlen kann man etwa bauen, indem man die ersten n:= |Σ| Primzahlen p_i mit den Elementen von Σ identifiziert und weiter q= ∏ _i=1ⁿp_i definiert. Die Abbildung eines Wortes w= a_i1a_i2…a_im auf ∑ _j=1^mp_ijq^j ist wegen der Eindeutigkeit der Primfaktorzerlegung injektiv. Es ist etwas schwieriger zu zeigen, dass diese Abbildung auch surjektiv ist, aber das soll uns jetzt nicht kümmern.

Potenz eines Worts: aⁱ lässt sich induktiv definieren als (a) a⁰ = ϵ, (b) aⁱ = a∙a^i-1.

Formale Sprache über Σ: Eine Teilmenge von Σ^*. Das ist die zentrale Definition in unserem Kurs, sie sagt nämlich, worüber wir reden wollen.

Wortproblem: Beim Wortproblem sucht man eine Funktion, die wahr zurückgibt, wenn ein Wort zu einer Sprache gehört, falsch sonst.

Berechenbarkeit: Eine Funktion, die nach endlich vielen Berechnungsschritten (wir müssen natürlich eigentlich noch erklären, was das ist, aber das muss vorerst warten) garantiert ein Ergebnis liefert, heißt berechenbar.

Entscheidbarkeit: Eine Sprache, deren Wortproblem berechenbar ist, heißt entscheidbar.