35. Berechenbarkeit

Turingmaschinen sind sehr allgemeine Konstrukte. Glaubenssatz:

Church’sche These: Die Klasse der “intuitiv” berechenbaren Funktionen stimmt mit der der Turing-berechenbaren Funktionen überein oder: Turing-Maschinen können alles, was Computer können (die Umkehrung ist sofort offensichtlich, wenn wir ein Programm zur Simulation einer Turing-Maschine schreiben können, und das geht schon für recht simple Systeme, z.B. T_EX).

Dabei heißt eine (partielle) Funktion f:Σ^*→Σ^*Turing-berechenbar, wenn es eine (deterministische) Turing-Maschine M gibt, so dass f(x) = y genau dann, wenn Sx * →#Zy# mit Z Endzustand von M.

Wir verwenden das Symbol * → hier etwas schlampig – es soll hier natürlich heißen “es gibt eine Zustandsfolge, die die linke in die rechte Seite überführt”. Wichtig ist, dass keine Aussage über das Verhalten der Maschine an den Stellen gemacht wird, an denen f nicht definiert ist.

Die charakteristische Funktion χ_M einer Menge M⊆N ist

die halbe charakteristische Funktion χ‘_M ist

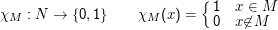
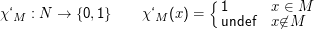
Beispiel: Sei L eine Chomsky-0-Sprache. Für jedes w∈L stoppt eine Turingmaschine mit L= L(M). Also sind die charakteristischen Funktionen

• χ_L:L→{0,1} konstant eins, also berechenbar;
• χ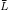:Σ^*→{0,1} nicht berechenbar, weil für x∈Σ^*\L das Verhalten von M nicht definiert ist
• χ‘_L:Σ^*→{0,1} berechenbar, weil das Verhalten nur für x∈L entscheidend ist.

Eine Sprache L heißt entscheidbar, wenn ihre charakteristische Funktion berechenbar ist, semi-entscheidbar, wenn ihre halbe charakteristische Funktion berechenbar ist.

Eine Sprache L heißt rekursiv aufzählbar, wenn L= ∅ oder eine (totale) berechenbare Funktion f:ℕ →Σ^* existiert, so dass L= {f(1),f(2),…}.

Satz: L rekursiv aufzählbar ⇔L semi-entscheidbar.

Beweisidee: “⇒”: Der Algorithmus prüft einfach alle f(i) durch.

“⇐”: Wir definieren zunächst w:ℕ →Σ^* (das geht, weil Sternbildung sehr simpel und Σ endlich ist). Sei χ‘_L durch den Algorithmus M realisiert. Wir nehmen ein Wort a∈L als “default” und definieren eine Funktion

Wenn wir die zwei Parameter von f in eine natürliche Zahl verpacken (es gibt rekursiv berechenbare Funktionen, die das können), haben wir die gewünschte Aufzählungsfunktion.

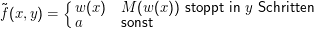
Anmerkung: Der Unterschied zwischen rekursiver Aufzählbarkeit und Abzählbarkeit ist, dass bei der Abzählbarkeit nicht die Berechenbarkeit der Bijektion gefordert ist (wichtig bei Teilmengenbildung!).