Das Wortproblem
Ist L(G) entscheidbar?
Ja für 1, 2, 3. Für Chomsky-3 ist das Wortproblem sogar in linearer Zeit lösbar. Ansonsten Argument über zunehmende Länge der Ableitungen – die Zahl der möglichen Vorgänger eines Wortes ist endlich. Das Wortproblem für Chomsky-1 ist allerdings mindestens NP-hart.
Nein für 0 (das Wortproblem für Chomsky-0-Sprachen ist nur semi-entscheidbar).
Das Leerheitsproblem
Ist L(G) = ∅ berechenbar?
Ja für 2 und 3. Bei 3 kann man allen Pfaden im DEA folgen und sehen, ob wenigstens einer in einem Endzustand landet. Bei 2 in CNF werden erst alle Nonterminale in einer Regel A→a markiert, dann alle Nonterminale in A→BC, wenn B und C schon markiert sind. Wenn am Ende S markiert ist, ist die Sprache nicht leer. Auf diese Weise kann man übrigens auch Parser bauen: CYK-Parser.
Nein für 0 und 1.
Das Endlichkeitsproblem
Ist |L(G)|<∞ berechenbar?
Ja für 2 und 3. Suche nach Zyklen in den zugehörigen Automaten oder Verwendung des Pumping Lemma (wenn es ein Wort über der Schranke um Pumping Lemma gibt, ist die Sprache unendlich aufpumpbar, es müssen also nur endlich viele Wörter geprüft werden).
Nein für 0 und 1.
Das Äquivalenzproblem
Ist L(G1) = L(G2) berechenbar?
Ja für 3, weil unter Schnitt, Vereinigung und Komplementbildung abgeschlossen. Da
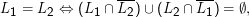
Nein für 0, 1 und 2. Für deterministisch kontextfreie Sprachen ist es allerdings entscheidbar.
Die Behauptungen, für die hier keine Argumente angegeben sind, sind eher schwierig zu beweisen. Häufig eine wichtige Rolle dabei spielt ein weiteres unentscheidbares Problem, das in der theoretischen Informatik an vielen Stellen lauert: Das Post’sche Korrespondenzproblem (PCP), zu dem später in diesem Skript noch etwas mehr gesagt wird.