37. Das Halteproblem

Sei Σ = {a₁,…,a_n} und Φ = {Z₁,…,Z_n}. Wir können statt Zeichen bzw. Zuständen auch ihre Indizes verwenden. Den Turing-Übergang

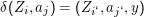
$δ(Z ,a ) = (Z ,a ,y) i j i‘ j‘$

können wir schreiben als

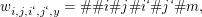
$w = ##i#j#i ‘#j ‘#m, i,j,i‘,j‘,y$

wobei die Zahlen binär dargestellt sind und m= 0,1,2 ist, wenn y= ⊲,⊳,∘.

Schließlich kodieren wir

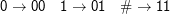
$0 → 00 1 → 01 # → 11$

Damit haben wir Turingmaschinen injektiv auf die Sprache {0,1}^* abgebildet und damit auf die natürlichen Zahlen.

Es gibt Turingmaschinen, die diese Darstellung ausführen können; “programmierbare Turingmaschine”, universelle Turingmaschine.

Das spezielle Halteproblem ist die Sprache

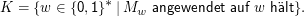
$* K = {w ∈ {0, 1} |Mw angewendet auf w h¨alt}.$

Es gibt dabei das Problem, dass nicht jedes Element von {0,1}^* eine Maschine kodiert (die Abbildung der Turingmaschinen in die natürlichen Zahlen ist injektiv, aber nicht surjektiv). Wir umgehen es, indem wir definieren, dass eine (beliebige) “Fallback-Maschine” 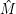ˆ
M läuft, wenn wir gerade keine gültige Maschinenkodierung haben (auf diese Weise wird die Abbildung surjektiv, aber nicht mehr injektiv – dafür ist die von den natürlichen Zahlen in die Turingmaschinen injektiv, und das zählt in dieser Definition).

Satz: Das spezielle Halteproblem ist nicht entscheidbar.

Beweis: Angenommen, K ist entscheidbar. Wir bauen eine Maschine M, die χ_K berechnet und eine weitere Maschine M‘, die stoppt, wenn M 0 ausgibt und sonst endlos läuft. M‘ ist eine Turingmaschine und kann daher durch das Wort w‘ ∈ {0,1}^* ausgedrückt werden. Wir wenden M‘ auf w‘ an:

Dann gilt:

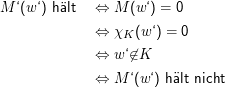
$M ‘(w ‘) h¨alt ⇔ M (w‘) = 0 ⇔ χK (w‘) = 0 ⇔ w ‘<ignored>⁄∈</ignored>∉K ⇔ M ‘(w ‘) h ¨alt nicht$

Diese Argumentation braucht keine Turingmaschine, sondern lediglich die Selbstanwendbarkeit. Möge folgender (geeignet ergänzter) C-Quelltext als haelt.c gespeichert sein:

int haelt(char *prog, char *in)
/* gibt 1 zurück, wenn das C-Programm prog auf der Eingabe in
hält, sonst 0 */
{ /* gibt es nicht :-) */
}

int main(void)
{ char *mysource = readFile("haelt.c");

  if (haelt(mysource, mysource)) while (1);
  return 1;
}

geht genauso: Wenn das Halteproblem entscheidbar ist, muss haelt(mysource, mysource) eins zurückgeben und damit main in eine Endlosschleife treiben. Dann aber dürfte haelt keine eins zurückgeben, weil das Programm ja nicht terminiert.

Das allgemeine Halteproblem ist die Sprache

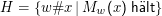
$H = {w#x |Mw (x) h¨alt}$

Satz: Das allgemeine Halteproblem ist nicht entscheidbar.

Beweis: Rückführung auf spezielles Halteproblem: Schon w#w ist nicht entscheidbar.

Auch das Halteproblem auf leerem Band ist nicht entscheidbar.

Zurück: Entscheidbarkeitsprobleme

Inhalt

Weiter: Ergänzung: PCP I

Index

Markus Demleitner