38. Ergänzung: PCP I

Mit die bequemste Methode, die Unentscheidbarkeit etlicher Probleme der Theoretischen Linguistik nachzuweisen, bedient sich des so genannten Post’schen Korrespondenzproblems PCP.

Beim PCP hat man eine endliche Folge von Wortpaaren K= (< v_i,w_i >)_i=1,…,n und sucht eine Folge von Indizes i_k ∈ {1,…,n}, so dass

gilt. Man möchte also aus einander entsprechenden Wortbruchstücken gleiche Wörter aufbauen.

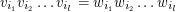
Beispiel: Mit K= (< 1,101 >,< 10,00 >,< 011,11 >) ist eine Lösung des PCP (1,3,2,3). Das kann man durch Einsetzen überprüfen:

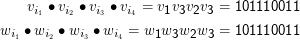
Wir können zeigen: Das so harmlos aussehende PCP ist unentscheidbar. Dazu braucht man den folgenden Begriff:

Seien A⊂Σ^* und B⊂Γ^* Sprachen. Dann gilt A≤B (“A ist auf B reduzierbar”), wenn

mit f: Σ^* →Γ^* total und berechenbar.

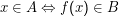
Reduzierbarkeit bedeutet insbesondere, dass die charakteristische Funktion von A einfach χ_B ∘f ist, also die Verkettung des eben definierten f mit der charakteristischen Funktion von B. Ist nun letztere berechenbar, so ist es auch χ_A. Das bedeutet aber weiter, dass sich (Semi-) Entscheidbarkeit durch die Reduktion von Problemen durchzieht.

Indem wir nun eine totale und berechenbare Funktionen angeben (oder eher so tun, als ob), die das PCP auf das Halteproblem reduziert, können wir aus der Unentscheidbarkeit des Halteproblems auf die des PCP schließen.

Diese Reduktion ist vor allem ein technisches Problem, bei dem zunächst das PCP auf ein modifiziertes Problem, das MPCP, bei dem i₁ = 1 gefordert wird, reduziert wird. Es ist nicht überraschend, dass das PCP auf das MPCP reduziert werden kann, da ja die Reihenfolge der Paare in der Folge kaum Einfluss auf die Lösbarkeit haben dürfte und durch Umordnung i₁ = 1 immer erreicht werden kann. Diese Argumentation hat allerdings Lücken, ein soliderer Beweis findet sich bei Schöning im Kapitel 2.7.

Satz: H ≤ MPCP (H steht dabei für das Halteproblem).

Zum Beweis lassen wir das MPCP die Folge der Konfigurationen der Turingmaschine M angesetzt auf w erzeugen und sorgen dafür, dass gleiche x= x₁ ∙x₂ ∙∙x_n und y nur dann herauskommen können, wenn M in einem Endzustand ist.

Dazu setzen wir K= (<$,$z₀w$ >,…). Dabei ist $ ein Trennzeichen, das sonst nicht im Bandalphabet von M vorkommt und z₀ der Startzustand von M. Das bewirkt, dass in y zu Anfang die Anfangskonfiguration steht, während x im Wesentlichen leer ist.

Die restlichen Paare ergeben sich aus der Definition von M. So dürfen wir etwa das Band von y nach x “kopieren”, indem für alle a∈Σ ein < a,a > zu K hinzugefügt wird.

Wo wir einen Zustand haben, müssen wir die Änderung von einer zur anderen Konfiguration übernehmen, indem etwa aus δ(z,a) = ⟨z‘,c, ⊳⟩ ein Paar wie < za,cz‘ > in K wird. Beachtet, wie hier das Verhalten der Turingmaschine simuliert wird. Man braucht drei Schablonen dieser Art plus ein paar weitere, weil wir am Anfang und am Ende jeder Konfiguration jeweils ein etwas anderes Verhalten brauchen, um unser Trennzeichen $ einzufügen.

Ist M in einem Endzustand, können wir den Bandinhalt löschen, etwa durch die Paare < az_e,z_e > und < z_ea,z_e > in K. Dabei ist a∈Σ und z_e ∈F.

Wenn dann nur noch der Endzustand in der Konfiguration steht, lassen wir x aufholen, was durch Anhängen von < z_e $$,$ > an K erreicht wird.

Die Idee des ganzen Spiels ist, dass zu jeder Zeit während der Lösung des MPCP

ist. Dabei sind die k_i jeweils gültige Konfigurationen von M, und an den jeweils letzten wird gerumgedoktort. x ist also immer um eine Konfiguration kürzer als y– bis eben ganzu zum Schluss, wenn durch < z_e$$,$ > zwei Trennzeichen an x kommen. Zu diesem Zeitpunkt haben die Löschregeln bereits dazu geführt, dass in y alles leer ist.

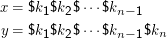
Den vollen Regelsatz gibt es wieder im Kapitel 2.7 des Schöning.