Das PCP lässt sich auf viele Probleme, die im Zusammenhang mit Sprachen auftreten, reduzieren. Das Prinzip ist dabei die Zuordnung zweier Grammatiken G1 und G2 über Σ1 = Σ2 = {0,1,$,a1,…,an} zum PCP K= (< xi,yi >)i=1…n mit xi,yi ∈{0,1}* wie folgt:
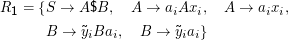
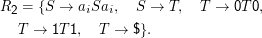
Dabei läuft i jeweils von 1 bis n, und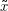 
ist die Umkehrung von x– z.B. ist für x= abc dann 
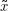= cba. Diese
Grammatiken wurden so konstruiert, dass sie eine Abbildung des PCP erlauben. Dazu betrachtet man die erzeugten
Sprachen:
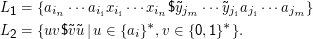
Die Elemente von L2 sind gerade die an $ “symmetrischen” Wörter, die von L1 gerade die, in denen Kandidaten für Lösungen des PCP rechts und links vom $ stehen (y ist dabei gespiegelt). Der Schnitt der beiden Sprachen sind die symmetrischen Wörter, bei denen rechts und links Kandidaten für die Lösung zum PCP stehen – und weil sie symmetrisch sind, sind die Kandidaten tatsächlich Lösungen.
Damit gilt: Das PCP ist auf das Schnittproblem L1 ∩L2 ? =∅ für kontextfreie Sprachen reduzierbar, letzteres ist daher nicht entscheidbar.
Ebenfalls nicht entscheidbar ist: Ist eine CFG G ambig?
Sei nämlich L(G3) = L1 ∪L2. Wegen der Abgeschlossenheit der CFGs unter Vereinigung ist auch G3 eine CFG. Sie ist ambig genau dann, wenn ein Wort sowohl eine Ableitung in G1 als auch in G2 hat, denn diese sind notwendig verschieden. Dies ist aber dann so, wenn L1 ∩L2≠∅.
Weiter sind unentscheidbar: L(G) kontextfrei? L(G) regulär?
Für kontextsensitive Sprachen ist schon das Leerheitsproblem L(G) ?=∅ nicht entscheidbar. Das liegt an der Abgeschlossenheit dieser Sprachen gegen Schnitt. Wäre das Leerheitsproblem für G entscheidbar, müsste es auch das Schnittproblem für L(G1) und L(G2) mit L(G) = L(G1) ∩L(G2) sein.