4. Technik: Zahlensysteme

Wir wollen uns in dieser Veranstaltung auf die Maschine zubewegen. Um zu verstehen, wie Computer wirklich mit Zahlen umgehen, muss man bedenken, dass sie nicht zehn, sondern nur einen Finger haben. Deshalb stellen sie Zahlen anders dar als wir.

“Normale” Zahlen, nämlich Dezimalzahlen, sind zur Basis 10 geschrieben:

– eine Zahl wird dargestellt als Summe von Beiträgen von Zehnerpotenzen.

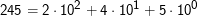
Computer setzen Zahlen als Summen von Zweierpotenzen zusammen:

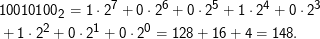
Binärzahlen sind also Folgen von Nullen und Einsen, ganz wie Dezimalzahlen Folgen von Dezimalziffern sind. In diesem Skript werden wir Binärzahlen immer mit einem Index 2 notieren.

Um Binärzahlen in Dezimalzahlen zu wandeln, fängt man also an, von rechts bei Null anfangend die Ziffern durchzuzählen und multipliziert die Ziffer jeweils mit der entsprechenden Zweierpotenz.

Vier binäre Ziffern können Zahlen zwischen 0 und 15 beschreiben, und zwei von diesen Vierergruppen sind ein Byte (nämlich 8 bit). Kompromiss zwischen Länge und Computergerechtigkeit: Hexadezimalziffern (besser: Sedezimalziffern). 0-9 werden erweitert um A-F (A=10F=15), und dann ist

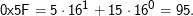
Dies ist offenbar ganz analog zum Vorgehen bei Binärzahlen; nur ist eben die Basis 16 und nicht Zwei, und entsprechend werden Sechzehnerpotenzen und nicht Zweierpotenzen verwendet.

Das Hin- und Herrechnen zwischen Zahlensystemen ist mühsam, einE guteR ProgrammiererIn sollte aber wenigstens für die 16 Hex-Ziffern die Bitmuster von 0 = 0000 bis F = 1111 sowie die ersten paar Zweierpotenzen (vielleicht bis 1024) im Kopf haben – es hilft sehr beim Analysieren von Problemen, die einem die Maschine so bereitet.

Es ist trivial, Konversionsfunktionen von Hex oder Binär nach Dezimal zu schreiben (in Python tuts auch "%d"%0xbaba). Für sedezimale Zahlen in Strings könnte folgender Python-Code verwendet werden:

def hexToInt(hexStr):
  res = 0
  for digit in hexStr:
    res *= 16
    if digit in string.digits:
      res += int(digit)
    elif digit in string.ascii_lowercase:
      res += ord(digit)-ord('a')+10
    elif digit in string.ascii_uppercase:
      res += ord(digit)-ord('A')+10
  return res

– kompliziert ist das eigentlich nur, weil wir Groß- und Kleinbuchstaben verarbeiten wollen (wie könnte das mit einem Dictionary implementiert werden?)

Die umgekehrte Prozedur ist auch nicht schwer, wenn man “von hinten” anfangen darf (Python macht es uns hier einfach):

def intToHex(number):
  res = []
  while number>0:
    curRem = number%16
    res.append(string.hexdigits[curRem])
    number /= 16
  res.reverse()
  return "".join(res)

Präfixe

Es ist:

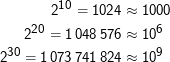
Wegen dieser bequemen Nähe haben Leute angefangen, 2¹⁰ Bytes als “Kilobytes” zu bezeichnen und analog für Mega und Giga. Das Problem ist, dass Kilo exakt für 10³ steht und, wenns drauf ankommt, Konfusion herrscht. In diesem Skript halten wir uns an die IEC-Konvention, nach der binäre Vielfache mit einem i gekennzeichnet sind. Es sind also 1kB = 10³ Bytes, aber 1kiB = 2¹⁰ Bytes und so fort für MB, MiB, GB und GiB.

Gesprochen werden soll kiB übrigens als “kibibyte”. Ich kenne aber niemanden, der/die das tut.