Vorzeichen
Ganze Zahlen können wir einfach in Bits speichern. Was machen wir mit dem Vorzeichen? Drei Methoden wurden versucht, alle “reservieren” das MSB (most significant bit, das höchste bit) – sie unterscheiden sich in der Interpretation der anderen Bits.
Signed Magnitude: Negation einer Zahl durch Flippen des MSB. Damit sind 100000002 und 000000002 Null. Arithmetik schwer zu bauen.
Einerkomplement: Negation einer Zahl durch Flippen aller Bits, -51 wäre dann 110000112, weil 001111002 51 ist. Auch hier ist Arithmetik schwierig und sowohl 0x00 als auch 0xff sind 0.
Zweierkomplement: Negation einer Zahl durch Berechnung des Einerkomplements und addieren von 1. Jetzt gibt es nur eine Null, deren Negation 111111112 + 1 = 100000000 ist. Das neunte Bit speichern wir nicht, wir sind also wieder bei der Null. Implementation in Hardware ist einfach.
Die Einfachheit der Implementation ergibt sich vor allem aus dem Umstand, dass etwa bei einer Addition keine Rücksicht auf das Vorzeichenbit genommen werden muss – im schlimmsten Fall ergibt sich ein “Überlauf”, weil das Ergebnis nicht mehr mit der gegebenen Zahl von Bits darstellbar ist. In diesem Fall funktioniert die Zweierkomplementdarstellung aber immerhin so, dass durch Addition oder Subtraktion der größten bzw. kleinsten darstellbaren Zahl das richtige Ergebnis herauskommt.
Ein Beispiel: 33 - 97 = -64. Ihr könnt leicht ausrechnen, dass
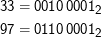
Um nun die Zahlen zu addieren, geht man wie in der Grundschule vor: Man schreibt die beiden Zahlen untereinander und addiert die Stellen von links nach rechts. Wenn man 1 + 1 rechnen muss, kommt 0 heraus und man hat einen Übertrag von 1 auf die nächste Stelle, muss man 1 + 1 plus einen Übertrag berechnen, bekommt man 1 und einen Übertrag.
Das Ganze kann dann so aussehen:
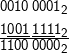
Dabei habe ich Stellen mit Übertrag durch einen Unterstrich markiert. Das Ergebnis ist negativ (das MSB ist gesetzt). Um herauszubekommen, was es ist, ziehen wir eins ab. Das entspricht der Addition von -1 = 111111112, was auf 1011 11112 führt, wobei wir den hier eigentlich anfallenden Übertrag auf der höchsten Stelle – das ist der schon erwähnte Carry – ignorieren. Jetzt flippen wir die Bits und kommen auf 010000002 oder einfach 64. Das Ergebnis unserer Rechnung war also wirklich -64.
Natürlich funktioniert das auch mit 16- oder 32-bittigen Zahlen ganz analog. Das Zweierkomplement hat leider die Falle, dass es nicht gleich viele positive wie negative Zahlen gibt. Die größte darstellbare positive Zahl (wieder für ein Byte) ist 011111112, nämlich 127. Das Zweierkomplement davon ist 100000012, nämlich -127 in Zweierkomplementdarstellung. Davon kann man offenbar noch eins abziehen, um auf 100000002 zu kommen, -128 in Zweierkomplementdarstellung. Das Zweierkomplement davon ist wiederum 011111112 + 1, mithin 100000002, also unser bekanntes -128. So etwas kann einen beißen (es bedeutet, dass etwas so harmloses wie der Ausdruck -a für bestimmte a “nicht funktionieren” kann). Beim Umgang mit negativen Zahlen am Rande des vom jeweiligen Typ darstellbaren Bereichs ist das zu bedenken.
Anmerkung: Python hat solche Probleme natürlich nicht, weil Bitmuster und Interpretation im Wert zusammenhängen. Früher konnte man zu große Integer einfach nicht konstruieren, mittlerweile schaltet Python bei einem Überlauf der Integer automatisch auf Long um. Das heißt nicht, dass es hier keine Probleme mit dem Zweierkomplement gäbe – sie tauchen z.B. im Zusammenhang mit großen Integer-Literalen auf. Wer will, kann sich das in PEP 237 ansehen, sucht nach oct literals.
Sign Extension
Toll an der Zweierkomplementdarstellung ist auch, dass, wenn die Zahlen klein genug sind, man einfach “oben” Bits wegstreichen kann und die Zahlen gleich bleiben, egal, ob die Bits 0 oder 1 sind. So ist -1 in 16 bit 0xffff, in 8 bit 0xff.
Das scheitert natürlich dann spektakulär, wenn die Zahl betragsmäßig zu groß ist – -180 kann natürlich nicht in 8 bit-Zweierkomplement dargestellt werden. Es ist nicht schwer, zu sehen, wann das nicht mehr klappt: Dann nämlich, wenn nicht alle bits über dem MSB der kleineren Darstellung den Wert des MSB der größeren haben.
Das macht den umgekehrten Weg etwas schwierig: Will man mehr Bits haben, muss man “oben” Kopien des Sign Bits anhängen. Aus 0xa0 (das ist -0x60, also -96 – rechnet es nach) muss 0xffa0 werden, aus 0x60 hingegen 0x0060.
Der C-Compiler macht das richtig; so genannte Sign Extension Bugs schleichen sich allerdings bei unüberlegter Kombination von signeds und unsigneds ein.
Fließkommazahlen
Fließkommazahlen bestehen aus Mantisse und Exponent. In einer Zahl wie 1.23456 × 104 ist die Mantisse dabei 123456 und der Exponent 4. Dabei stellt der Rechner die Zahlen natürlich wieder binär dar.
Die üblichen IEEE-floats machen Signed Magnitude. Von 32 bits ist einer das Vorzeichen, 8 der Exponent plus 127 und 23 die Mantisse, die nach dem ersten gesetzten Bit gespeichert wird.
Das Ganze gibt es auch noch für doubles, die in 64 bits mit 11 bits für den Exponenten (plus 1023) und 52 bits für die Mantisse gespeichert werden. Wenn ihr das abschätzt, ergeben sich in etwa die Wertebereiche und Genauigkeiten, die auf der letzten Folie angegeben sind – etwas mehr als 3 Binärstellen entsprechen einer Dezimalstelle (weil 3 bits gerade 8 Ziffern darstellen können), d.h. 22 bits sind weniger als 22∕3 ≈ 7 Stellen, die 51 bits entsprechend weniger als 17 Stellen.
Was den Exponenten angeht, kann man entweder 256 oder 2048 verschiedene Werte speichern. Allerdings sind das natürlich Exponenten für binäre Mantissen. Weil eine Binärstelle wieder knapp einer Drittel Dezimalstelle entspricht, haben wir dezimal einen Wertebereich von ungefähr 85 oder 680 – wenn man das halbiert, ist man ungefähr bei den -38 bis 38 und -308 bis 308 (dass es nicht genau stimmt, liegt wieder daran, dass man etwas mehr als drei Bits für ein Dezimalzeichen braucht).
Wer will, kann sich das mit Hilfe von Quanfei Wens IEEE-754 Calculator genauer ansehen.
Übrigens werden in Anwendungen, in denen man auf Genauigkeit verzichten kann, aber dafür eine exakte Repräsentation von Dezimalzahlen braucht (das ist im Groben vor allem der Finanzsektor) auch gerne andere Darstellungen reeller Zahlen verwendet. Am bekanntesten sind wohl die Binary Coded Decimals (BCDs), in der jeweils vier Bit verwendet werden, um eine Dezimalziffer zu speichern.