3. Data types

3.1. Overview

pgSphere provides spherical data types for storing with PostgreSQL. Furthermore, there is a data type to do transformations.

3.2. Point

• sites on earth

• star positions on the sky sphere

• spherical positions on planets

A spherical point (or position) is given by two values: longitude and latitude. Longitude is a floating point value between 0 and 2π. Latitude is a floating point value, too, but between -π/2 and π/2. It is possible to give a spherical position in degrees (DEG) or with a triple value of degrees, minutes and seconds (DMS). Degrees and minutes are integer values. The seconds are represented using a floating point value. A fourth method is specifying a longitude value as a triple value of hours, minutes and seconds (HMS). But, you can not use it with latitude values.

sql> SELECT spoint '(0.1,-0.2)';
              

sql> SELECT spoint '( 10.1d, -90d)';
              

sql> SELECT spoint '( 10d 12m 11.3s, -13d 14m)';
              

sql> SELECT spoint '( 23h 44m 10s, -1.4321 )';
              

As you can see you can combine the input format for longitude and latitude. The value pairs are always enclosed within braces. Spaces are optional.

3.3. Euler transformation

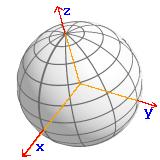
• spherical object transformations

• spherical coordinates transformations

The input syntax of an Euler transformation is:

angle1, angle2, angle3 [, axes ]

where axes is an optional 3 letter code with letters : X, Y, or Z. Default is ZXZ. angleN is any valid angle with the input format RAD, DEG, or DMS.

To do a transformation, you have to use a transformation operator (see Section 5.10).

sql> SELECT strans '20d, -270d, 70.5d, XZY';
              

sql> SELECT strans '2d 20m, 10d, 0';
              

3.4. Circle

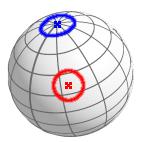
• sites on earth having a maximum distance from another site

• round cluster or nebula on sky sphere

• a position with an undirected position error

A circle is specified using a spherical point (spoint) and a radius :

< point , radius >

Valid radius units are RAD, DEG, and DMS. The circle radius must be less than or equal to 90° and cannot be less than zero.

sql> SELECT scircle '< (0d, 90d), 5d >';
              

3.5. Line

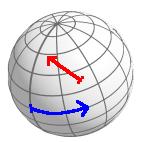
• direct connection of two points

• meteors on the sky sphere

To allow lines with a length larger than 180°, the input i syntax is a somewhat complex.

A general located line with a length length is defined as a line starting at position (0d,0d) and ending at position (length,0d) transformed with an Euler transformation euler. The input syntax is :

( euler ), length

sql> SELECT sline '( -90d, -20d, 200d, XYZ ), 30d ';
              

3.6. Ellipses

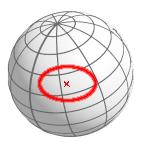
If the center of any spherical ellipse is the North Pole, the perpendicular projection into the x-y-plane gives an ellipse as in two-dimensional space.

Use cases are:

• cluster or nebula on the sky sphere where the `height' is lower than the `width'

• to describe a position error

An ellipse always has:

• a major radius rad_1

• a minor radius rad_2

• a center center

• a position angle pos (inclination)

Hence, the input syntax is:

< { rad_1, rad_2 }, center, pos >

sql> SELECT sellipse '< { 10d, 5d } , ( 20d, 0d ), 90d >';
               

3.7. Path

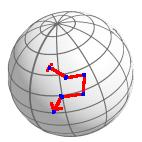
• rivers on earth

• trajectories of planets or comets on the sky plane

Paths within pgSphere are simplified lists of positions. The input syntax is :

{pos1,pos2[,pos3[,pos4[,...]]]}

sql> SELECT spath '{ (10d,0d),(45d,15d),(80d,30d) } ';
              

3.8. Polygon

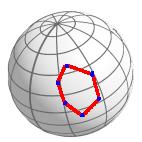
A spherical polygon is a closed spherical path where line segments cannot be crossed. One main use case are areas on the earth and sky sphere. Polygons within pgSphere have the same input syntax as paths:

{pos1,pos2,pos3[,pos4[,... ]]}

sql> SELECT spoly '{ (270d,-10d), (270d,30d), (290d,10d) } ';
              

3.9. Coordinates range

A spherical box is a coordinates range. Hence, you can select objects within a longitude range and latitude range. The box is represented using two spherical points: the southwest (pos_sw) and the northeast (pos_ne) edge of the box. The input syntax is:

( pos_sw, pos_ne )

or

pos_sw, pos_ne

sql> SELECT sbox '( (0d,20d), (0d,23d) )';
              

sql> SELECT sbox '( (350d,-10d), (10d,+10d) )';
              

3.10. smoc: HEALPix Multi-Order Coverage map

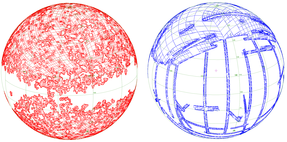
The datatype smoc allows one to define and manipulate any region of the sky in such a way that basic operations like union, intersection can be performed very efficiently. It is dedicated to VO applications or VO data servers for building efficient procedures for which mapping knowledge is required like generic catalog cross-match, computation of data set intersections, etc. This encoding method is called "Multi-Order Coverage map" or "MOC".

The goal behind the MOC is to get a spherical geometry description for any sky region in order to provide very fast and accurate union, intersection and equality operations between them. In order to accomplish this task, we based the system on a regular and hierarchical partitioning of the sphere, a process called tessellation, yielding pixels of different size. At level 0, the sky is divided into 12 pixels numbered 0 to 11. At the maximally defined level 29, there are 12 * 4^29 = 3458764513820540928 pixels.

The MOC standard is described at http://www.ivoa.net/documents/MOC/

level/pixel1-pixel2 [...] level/pixel1-pixel2 [...]

sql> SELECT smoc '0/';
              

sql> SELECT smoc '0/0-11';
              

sql> SELECT smoc '0/4 1/0 2 12-13 34-35 45 47 2/4 6 12 14 56-57 60-61 88 90-91 116-117 119 130-131 134-135 177 179 185 187';