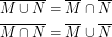Eine Menge ist eine ” Zusammenfassung von [… ] Objekten unserer Anschauung oder unseres Denkens“ (Cantor, 1895). Diese Definition ist schlecht, weil sie auf Widersprüche führt. Eine Definition der Menge, die tragfähig ist, ist aber kompliziert und interessiert hier nicht.
Mengen notieren wir in Großbuchstaben, ihre Elemente zählen wir in geschweifen Klammern auf: M1 = {1,3,5}, M2 = {rot,grün,gelb}, M3 = {x|x ist transitives Verb} (lies: M3 ist die Menge aller x mit der Eigenschaft, dass x ein transitives Verb ist).
B ist Teilmenge von A (B⊆A), wenn jedes Element von B auch in A enthalten ist, echte Teilmenge von A (in Zeichen: B⊂A), wenn es zusätzlich mindestens ein x∈A gibt, für das x∉B gilt.
Zwei Mengen sind gleich, wenn sie die gleichen Elemente haben: B⊆A∧A⊆B (Extensionalitätsprinzip)
Die leere Menge, ∅= {x|x≠x} hat kein Element.
Die Potenzmenge ℘(A) ist die Menge aller Teilmengen von A. Die Potenzmenge einer n-elementigen Menge hat 2n Elemente. ℘({a,b}) = {∅,{a},{b},{a,b}}
Operationen auf Mengen
Vereinigung: A∪B= {x|x∈A∨x∈B}.
Schnitt: A∩B= {x|x∈A∧x∈B}.
Differenz: A\B= {x|x∈A∧x∉B}.
Komplementbildung: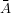 
= O\A= {x∈O|x∉A}. Dabei heißt O die Obermenge.
Rechenregeln
Hier steht ∘ für ∪ oder ∩
- Kommutativität: M∘N= N∘M
- Assoziativität: K∘(M∘N) = (K∘M) ∘N
- Idempotenz: M∘M= M
- Distributivität: K∪(M∩N) = (K∪M) ∩(K∪N) (und mit ∩ und ∪ vertauscht)
DeMorgan-Regeln:
