4. Wahrscheinlichkeit I

Intuitiv: Wenn ein Experiment bei 100 Versuchen im Mittel 30 Mal ein bestimmtes Ergebnis liefert, würden wir sagen, dieses Ergebnis habe eine Wahrscheinlichkeit von 30∕100, der relativen Häufigkeit. Das ist axiomatisch schwierig zu fassen, deshalb Zugang von der ”anderen Seite“.

Eine Ergebnismenge (auch Stichprobenraum, sample space) Ω ist eine endliche (tatsächlich darf sie auch abzählbar unendlich sein, aber um solche mathematischen Feinheiten kümmern wir uns erstmal nicht) Menge von Ergebnissen (Stichproben, Realisierungen, sample points, basic outcomes) eines Experiments. Ein Experiment kann dabei ziemlich viel sein: Das Werfen eines Würfels, die Bestimmung des Typs eines Worts, die Frage, ob ein Pixel schwarz ist oder nicht usf.

Teilmengen von Ω heißen Ereignis (event). Das Ereignis A⊂Ω ist eingetreten, wenn das Experiment ein Ergebnis ω∈A geliefert hat.

Sind A, B zwei Ereignisse, so ist

• A∪B das Ereignis, dass A oder B sich ereignen,
• A∩B das Ereignis, dass A und B sich ereignen,
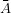• das Ereignis, dass sich A nicht ereignet,
• ∅ das unmögliche Ereignis,
• Ω das sichere Ereignis

Wenn A∩B= ∅, sind A und B unvereinbar.

Die Menge aller Ereignisse ist ℘(Ω). Eine Abbildung

heißt Wahrscheinlichkeitsmaß oder Wahrscheinlichkeitsverteilung (probablity function), wenn

• P(Ω) = 1 (Normiertheit)
• P(A) ≥0 für alle A∈℘(Ω) (Positivität)
• P(A∪B) = P(A) + P(B), wenn A∩B= ∅ (Additivität)

Vorsicht: Es gibt auch eine Verteilungsfunktion (distribution function) – die ist aber was ganz anderes. Unsere Verteilungen heißen auf Englisch Distribution oder, wenn Ω etwas wie die reellen Zahlen ist, auch gern probability density function (PDF, Wahrscheinlichkeitsdichte).

P(A) heißt Wahrscheinlichkeit von A. Das Paar (Ω,P) heißt Wahrscheinlichkeitsraum (probability space). Wahrscheinlichkeitsräume sind unsere Modelle für Experimente. In der Sprachverarbeitung ist die Wahl des geeigneten Modells häufig die schwierigste Aufgabe überhaupt. Einerseits ist klar, dass Sprache mit Zufallsexperimenten zunächst wenig zu tun hat, andererseits müssen meist eher gewagte Annahmen gemacht werden, um ein gegebenes Phänomen überhaupt einer statistischen Analyse zugänglich zu machen. Dass statistische Verfahren in der Sprachverarbeitung häufig so gut funktionieren, ist eigentlich eher überraschend.

In einem realen Experiment ist die absolute Häufigkeit eines Ereignisses k_n(A) die Zahl der Versuchsausgänge in A in den ersten n Versuchen, die relative Häufigkeit h_n(A) = k_n(A)∕n. Vorerst postulieren wir keinerlei Zusammenhang zwischen h_n und P.