Für ein Wahrscheinlichkeitsmaß P gelten
- P(
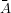 ) = 1 -P(A), speziell P(∅) = 0.
) = 1 -P(A), speziell P(∅) = 0. - A⊂B⇒P(A) ≤P(B).
- P(A\B) = P(A) -P(A∩B)
- P(A∪B) = P(A) + P(B) -P(A∩B).
- P(A) = ∑ ω∈AP(ω)
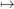 P(ω) nennen wir Wahrscheinlichkeitsfunktion.
P(ω) nennen wir Wahrscheinlichkeitsfunktion.
Wenn P(ωi) = P(ωj) für alle ωi,ωj ∈Ω, heißt P Gleichverteilung, das zugehörige Experiment Laplace-Experiment. Klassisches Beispiel für ein Laplace-Experiment ist das Würfeln mit einem fairen Würfel. Aber auch hinter Urnenmodellen steht ein Laplace-Experiment – wenn es ohne zu viel Krampf geht, ist es meistens vorteilhaft, ein gegebenes Problem als Laplace-Experiment zu formulieren.In Laplace-Experimenten ist P(ω) = 1∕|Ω| und P(A) = |A|∕|Ω| Die Schreibweise |A| bezeichnet die Kardinalität der Menge A, im endlichen Fall einfach die Zahl ihrer Elemente).
Wenn |Ω|= 2, heißt das Experiment Bernoulli-Experiment. Ein Element ωe heißt Erfolg, die zugehörige Wahrscheinlichkeit Erfolgswahrscheinlichkeit. Klassisches Beispiel ist hier der Münzwurf – ” Kopf“ könnte hier der Erfolg sein. Im Allgemeinen ist aber die Erfolgswahrscheinlichkeit ungleich 1∕2.
Beispiel Münzwurf: Ω = {0,1}, P(1) = 0.5, P(0) = 0.5. Dabei steht 1 etwa für ” Brandenburger Tor“ und 0 für ”Zahl“.
Beispiel Würfel: Ω = {1,2,3,4,5,6}, P(ω) = 1∕|Ω|= 1∕6. Mögliche Ereignisse wären ” Gerade Zahl“, A= {2,4,6} oder ”Größer als zwei“, B= {3,4,5,6}.
Beispiel drei Münzwürfe:
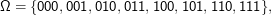
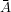 ) = 1 -P(A) ab.
) = 1 -P(A) ab.