Das Urnenmodell erleichtert häufig die Berechnung von Wahrscheinlichkeitsfunktionen. In einer Urne liegen nummerierte Kugeln und werden gezogen. Nach jedem Zug legt man entweder zurück oder nicht, und die gezogenen Kugeln werden entweder angeordnet oder nicht. Fertige Formeln für |Ω| bei Ziehung von n Kugeln aus N:
|
| mit Rücklegen | ohne Rücklegen | |||||
|
angeordnet |
I Nn |
II (N)n | |||||
|
nicht angeordnet |
IV ( n+ N-1 n ) |
III ( N n) | |||||
mit (N)n = N(N-1)
(N-n+ 1) = N!∕(N-n)! und dem Binomialkoeffizienten (das ist einfach eine Größe, die immer
wieder auftaucht und drum abgekürzt wird)
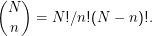
Wo kommen diese Formeln her?
In Reihenfolge mit Rücklegen: Wir ziehen n Mal, und auf jedem Platz gibt es N Möglichkeiten.
In Reihenfolge ohne Rücklegen: Wir ziehen n Mal; beim ersten Mal haben wir N Möglichkeiten, beim zweiten Mal noch N-1 usf., bis ich n Kugeln gezogen habe. Bei der letzten Ziehung habe ich also N-n+ 1 Möglichkeiten. – Spezialfall dazu: n= N, |ΩII |= N!. Das ist gerade die Zahl der Permutationen (also der verschiedenen Anordnungen) von N verschiedenen Dingen.
Ohne Reihenfolge ohne Rücklegen: Das ist praktisch ΩII, nur zählen alle verschiedenen Anordnungen der gleichen Zahlen als ein Element. Jede dieser Anordnungen kommt n!-mal vor, also |ΩIII|= |ΩII|∕n!.
Ohne Reihenfolge mit Rücklegen: Im Prinzip würde es reichen, alle Elemente von ΩI zu nehmen, und die mit identischen Elementen miteinander zu identifizieren. Die einfache Division durch die Größe einer solchen Äquivalenzklasse wie bei der Ableitung von |ΩIII| aus ΩII geht hier nicht, da z.B. {0,0} nur aus (0,0) kommt, während {0,1} sowohl aus (0,1) also auch aus (1,0) entsteht – die Klassen sind nicht alle gleich groß.
Deshalb Trick: Unser Versuchsergebnis stellen wir dar als eine Folge von n Einsen und N Nullen. Vor der i-ten Null steht für jede Ziehung der Kugel i je eine Eins. Die Stichprobe ” Zwei Mal nullte Kugel, Null Mal erste Kugel, Ein Mal zweite Kugel“ würde also zu 110010. Umwandlung in Urnenmodell: Wir ziehen die Positionen der Einsen aus einer Urne mit N+ n-1 Kugeln (die letzte Stelle darf keine Eins sein) ohne Zurücklegen und ohne Ordnung; das ist ΩIII, also ist |ΩIV |= (N+n-1 n ) .
Beispiel: Ziehen mit und ohne Rücklegen mit Reihenfolge 3 aus 4:
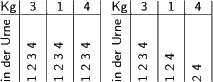
In der Zeile mit Kg steht dabei die jeweils gezogene Kugel, darunter die Kugeln, die noch gezogen werden können – mit Zurücklegen hat man immer vier Möglichkeiten, ohne Zurücklegen hat man immer weniger Auswahl. Wenn man das ein wenig formalisiert, kommt man auf die oben angegebenen Formeln.
Alternative Interpretation: Verteilung von Murmeln auf Plätze, die Nummer der gezogenen Kugel ist die Nummer des Platzes. Kann ein Platz mehrfach besetzt werden, ist ein Experiment mit Zurücklegen nötig, sind die Murmeln ununterscheidbar, spielt die Reihenfolge der Züge offenbar keine Rolle.
