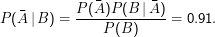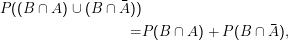7. Unabhängigkeit und bedingte Wahrscheinlichkeit

Zwei Ereignisse A und B heißen unabhängig, gdw. P(A∩B) = P(A)P(B). In der Realität wird man meistens argumentieren, die Ereignisse seien unabhängig und man dürfe die Formel deshalb so anwenden. Das Eintreten des einen Ereignisses beeinflusst also die Wahrscheinlichkeit des Eintretens des anderen nicht.

Was ist, wenn A und B nicht unabhängig sind?

P(A|B) heißt bedingte Wahrscheinlichkeit von A unter B, die Wahrscheinlichkeit, dass A eintritt, nachdem B schon eingetreten ist, und ist definiert als

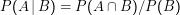
Diese Definition ist vernünftig. Wir wollen nur Ereignisse aus A betrachten, für die B schon eingetreten ist. Es können also nur noch die Stichproben aus A auftreten, die schon in B sind (deshalb A∩B). Außerdem hätte man gern, dass P(B|B) = 1 – wenn B schon eingetreten ist, ist B sicher, deshalb die Division durch P(B). Für unabhängige Ereignisse ist

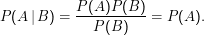
Natürlich ist diese Definition nicht anwendbar, wenn P(B) = 0.

Beispiel: Würfel. Es werde zwei Mal gewürfelt, A sei das Ereignis, dass beim zweiten Mal eine 1 fällt, B, dass beim ersten Mal eine 1 fällt. Der Stichprobenraum besteht also aus Tupeln (z₁,z₂) mit z₁,z₂ ∈{1,…,6}.

Offenbar ist P(A) = P(B) = 1∕6. Was ist P(A|B)? Es ist

Damit ist Wie erwartet, sind die Würfe unabhängig.

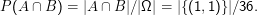
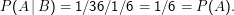
Werde nun ein Mal gewürfelt, B sei das Ereignis, dass eine gerade Zahl fällt, A, dass die Vier fällt. Es gilt:

Natürlich ist die Wahrscheinlichkeit, eine Vier zu finden, größer, wenn ich vorher schon weiß, dass eine gerade Zahl herausgekommen ist.

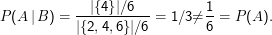
Ein anderes Beispiel: Sei Ω die Menge aller Texte am Netz (ein Text soll dabei einfach durch die Menge der in ihm vorkommenden Wörter repräsentiert sein), P(ω) = 1∕|Ω| für alle ω∈Ω. Wir interessieren uns für die Ereignisse A= {ω| Bundeskanzler ∈ω} und B= {ω| Schröder ∈ω} und nehmen an, dass google Ω ausschöpft, also für die Berechnung von |A|, |B| und |Ω| taugt. Dann ist

Die Wahrscheinlichkeit, dass ein Text das Wort Bundeskanzler enthält, wenn es das Wort Schröder enthält, ist also

während die Wahrscheinlichkeit, dass eine Webseite, die Bundeskanzler enhält, auch von Schröder redet ist. Interpretiert man Wahrscheinlichkeiten als relative Häufigkeiten, so folgt, dass etwa 15% aller Webseiten, die von Schröders reden, auch über Bundeskanzler reden, während umgekehrt fast die Hälfte aller Seiten, die von Bundeskanzlern erzählen, auch den Namen Schröder enthalten.

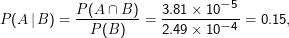
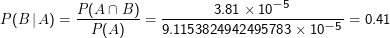
Umformung der Definition bedingter Wahrscheinlichkeit:

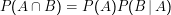
Weil Vereinigung kommutiert, ist das auch gleich P(B)P(A|B). Zusammen Bayes’sche Umkehrformel:

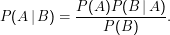
Beispiel: Sei A das Ereignis, dass eine bestimmte Person die Krankheit Burizystose hat, B das Ereignis, dass der der Plutopharma-Test der Sachse AG anschlägt. Es sei P(A) = 0.001, P(B|A) = 0.9 und die Wahrscheinlichkeit, dass der Test bei Nichtinfizierten positiv ausfällt, P(B|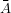) = 0.01. Die Wahrscheinlichkeit, dass jemand infiziert ist, wenn der Test positiv ausfällt, ist

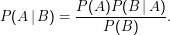
P(B), die Wahrscheinlichkeit, dass ein Test ohne Kenntnis des Gesundheitszustands des Probanden positiv ausfällt, kennen wir nicht. Wir können sie aber ausrechnen:

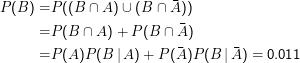
Jetzt P(A|B) = 0.001 ⋅0.9∕0.011 = 0.08, die Wahrscheinlichkeit, dass jemand gesund ist, wenn der Test positiv ausfällt: