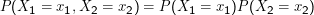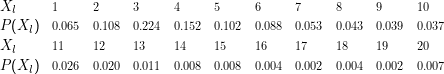8. Zufallsvariable

Eine Zufallsvariable (random variable) ist eine Funktion X:Ω →ℝⁿ.

Beim Würfeln kann die Zufallsvariable die Augenzahl sein, bei zwei Würfen etwa die Summe der Augenzahlen (so dass die Stichprobe (1,3) auf 4 abgebildet wird) oder 0 für einen Pasch und 1 für einen Nicht-Pasch. Bei zufällig ausgewählten Personen könnten Zufallsvariablen das Alter, die Größe oder das Bruttoeinkommen sein, bei Wörtern ihre Länge, bei Zeichen ihr ASCII-Code, beim Münzwurf 0 für Blatt und 1 für Zahl.

Wir werden später das mit dem ℝⁿ nicht mehr so eng sehen und z.B. auch Wörter als Zufallsvariablen akzeptieren. Dann werden aber Begriffe wie Erwartungswert (nächste Folie) sinnlos, weswegen wir das vorerst mal nicht tun.

Schreibweise:

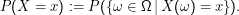
Darstellung der Verteilung (probability mass function, pmf, frequency function) P_X(x) = P(X= x) von Zufallsvariablen (die dadurch definierte Wahrscheinlichkeit dafür, dass bei einem Experiment die Zufallsvariable X den Wert x erhält, ist also einfach die Summe der Wahrscheinlichkeiten aller Stichproben ω, die von X auf x abgebildet werden) in Histogrammen, hier für die Wortlänge in einem englischen (links) und deutschen (rechts) Text:

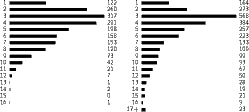
Natürlich ist das nicht wirklich das Histogramm einer Zufallsvariablen. Diese muss nämlich aus einem Modell kommen und nicht aus einer Beobachtung von Häufigkeiten. Allerdings werden wir in Kürze endlich eine Verbindung zwischen den beiden Größen herstellen. Genau genommen sollten in das Histogramm auch die Werte von P(X= x) eingetragen werden und nicht die rohen Zählungen. Dieser Defekt wäre allerdings durch schlichte Division durch die Gesamtzahl der Beobachtungen leicht heilbar.

Sind mehrere Zufallsvariablen X₁,X₂,… auf einem Wahrscheinlichkeitsraum definiert – etwa die Gesamt-Augenzahl und die Anzahl der Würfe mit Ergebnis sechs beim n-fachen Würfeln –, so kann man sie zu einer gemeinsamen Zufallsvariable

zusammenfassen (das Ergebnis ist also etwas wie ein Vektor).

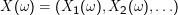
Beispiel: Zweimaliges Würfeln. Zufallsvariablen: Augensumme, X₁, Augen im ersten Wurf, X₂; X₁ läuft waagrecht, X₂ läuft senkrecht.

		2	3	4	5	6	7	8	9	10	11	12
1		1∕36	1∕36	1∕36	1∕36	1∕36	1∕36	0	0	0	0	0		1∕6
2		0	1∕36	1∕36	1∕36	1∕36	1∕36	1∕36	0	0	0	0		1∕6
3		0	0	1∕36	1∕36	1∕36	1∕36	1∕36	1∕36	0	0	0		1∕6
4		0	0	0	1∕36	1∕36	1∕36	1∕36	1∕36	1∕36	0	0		1∕6
5		0	0	0	0	1∕36	1∕36	1∕36	1∕36	1∕36	1∕36	0		1∕6
6		0	0	0	0	0	1∕36	1∕36	1∕36	1∕36	1∕36	1∕36		1∕6
		1∕36	2∕36	3∕36	4∕36	5_36	6∕36	5∕36	4∕36	3∕36	2∕36	1∕36

In der Mitte der Tabelle ist die gemeinsame Verteilung von X= (X₁,X₂), an den Rändern stehen die Marginalverteilungen P(X₁) und P(X₂). Dabei ist P(X₁) = ∑ _X2∈X2P(X₁,X₂) und analog für P(X₂).

Die Verteilungen X_n heißen 1-dimensionale Marginalverteilung (Randverteilung, marginal distribution) – sie entstehen durch Addition über alle nicht betrachteten Zufallsvariablen. Entsprechend lassen sich mehrdimensionale Marginalverteilungen definieren, z.B. (X₂,X₃) über der Gesamtvariablen (X₁,X₂,X₃) durch Summation über X₁.

Unabhängigkeit für Zufallsvariablen

Zwei Zufallsvariablen sind unabhängig, wenn für alle x₁,x₂

gilt (und analog für mehrfache Produkte).

Eine mögliche Verteilung der Zufallsvariablen X_l ” Wortlänge in einem deutschen Text“