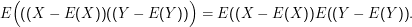9. Erwartungswert und Varianz

Der Erwartungswert (expectation) einer Zufallsvariablen X ist definiert als

Wenn X= {x₁,x₂,…,x_n} den Wertebereich von X bezeichnet, ist das gleichbedeutend mit

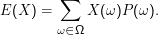
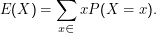
In der zweiten Form der Definition habe ich die Schreibweise

Damit ist auch klar, warum die beiden Formen äquivalent sind: In Wirklichkeit haben wir etwas betrogen, weil wir uns auf endliche Wertebereiche beschränkt haben, aber das funktioniert auch sonst.

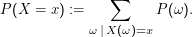
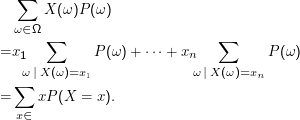
Anmerkungen:

1. Das entspricht einer Art mit den Wahrscheinlichkeiten gewichteten Mittelwert aller Werte, die die Zufallsvariable annehmen kann.
2. So etwas würde mit den Elementen von Ω zunächst nicht gehen, weil auf ihnen, selbst wenn wir sie 1, 2, 3 nennen, keine Arithmetik definiert ist. Deshalb kommt die Definition erst hier, obwohl ” Mittelwert“ ein eigentlich sehr natürlicher Begriff sind.
3. Die Schreibweise E(X) deutet an, dass E eine Funktion ist. Mit einem ausreichend allgemeinen Funktionsbegriff ist das auch so, im Allgemeinen aber bezeichnet man Funktionen, die Funktionen (hier das X) auf Zahlen abbilden, als Funktionale. Deshalb wird in der Literatur auch häufig EX oder E[X] für E(X) geschrieben. Uns braucht das nicht zu kümmern, solange wir im Kopf behalten, dass X eben keine Zahl ist.

Der Erwartungswert ist linear:

für ein λ∈ℝ.

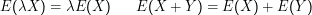
Wenn X und Y unabhängig sind, ist E(XY) = E(X)E(Y).

Die zweite Behauptung folgt aus

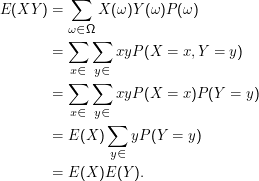
Dabei haben wir im Schluss von der zweiten auf die dritte Zeile die Unabhängigkeit ausgenutzt und im Schluss von der dritten auf die vierte Zeile einfach ausgeklammert (∑ _ixi= x∑ _ii). Das geht hier, weil x_i und y_i unabhängig voneinander variieren und keine Abhängigkeit der einzelnen Faktoren besteht.

Trotzdem haben hier etwas betrogen. X ist nämlich auch bei uns häufig nicht endlich, und wenn die Summen über abzählbar unendliche Mengen ausgeführt werden, sind die Operationen, die wir hier machen, nicht unkritisch – in der Tat funktioniert das aber auch streng.

Schließlich: Die Schreibweise λX soll einfach die Zufallsvariable bezeichnen, in der jeder Wert mit λ multipliziert wird. Ist etwa der Wertebereich von X, ” Augenzahl beim sechsseitigen Würfel“ {1,2,…,6}, ist der Wertebereich von 3X einfach {3,6,9,…,18}.

Beispiel: Sechsseitiger Würfel, X ist ” Augenzahl“:

Diese Aussage werden wir bald als ” Wenn wir wirklich oft würfeln, wird jeder Wurf im Mittel dreieinhalb Augen beitragen“ interpretieren können.

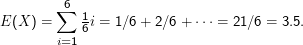
Nochmal Wortlängen X_l. Nach der Tabelle berechnet sich

Für einen englischen Text könnte E(X_l) = 4.62 sein.

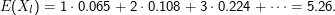
Varianz

Die Varianz einer Zufallsvariable X ist definiert als

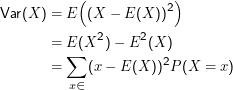
Die Varianz ist nicht linear: Var(λX) = λ²Var(X). Unter anderem deshalb arbeitet man gern mit ihrer Wurzel, der Standardabweichung σ_X = .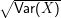

Momente

Allgemein heißt E(Xⁿ) n-tes Moment, E(X-E(X))ⁿ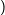 n-tes zentrales Moment. Der Erwartungswert ist also das erste Moment, die Varianz das zweite zentrale Moment.

Mehrere Variable, Kovarianz

Wenn X und Y unabhängig sind, gilt Var(X+ Y) = Var(X) + Var(Y)

Das lässt sich einsehen, wenn man das Argument des Erwartungswerts ausrechnet, der für Var(X+ Y) zu berechnen ist (dazu muss offenbar drei Mal die binomische Formel angewendet und die Linearität des Erwartungswerts genutzt werden):

Der erste Teil der letzten Zeile ist im Erwartungswert schon das Ergebnis, der zweite Teil im Erwartungswert Null: der erste Summand ist aber (und hier kommt die Unabhängigkeit) 2E(X)E(Y), der gesamte Ausdruck also Null.

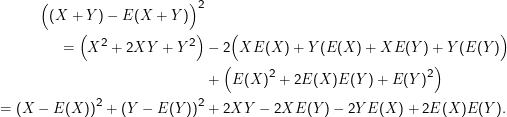
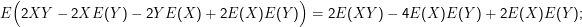
Sind X, Y Zufallsvariablen über Ω, so heißt

Kovarianz von X und Y. Sie ist ein Maß für die Ähnlichkeit der Verteilung. Als Korrelationskoeffizient wird die Größe bezeichnet.

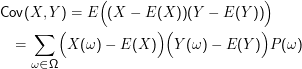
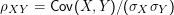
Die Kovarianz von unabhängigen Zufallsvariablen ist Null, denn mit X und Y sind auch X-E(X) und Y-E(Y) unabhängig, und daher ist

Wegen der Linearität des Erwartungswertes ist weiter E(X-E(X)) = E(X) -E(E(X)) = 0. Die Kovarianz ist also ein Maß dafür, wie groß die Abhängigkeit von X und Y ist.