10. Häufig auftretende Verteilungen

Binomialverteilung

Sei Ω = {u,d} der Stichprobenraum eines Bernoulli-Experiments, sei P(u) = p und P(d) = q= 1 -p. Wir betrachten den Stichprobenraum 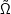= ⊗ _i=1ⁿΩ, also etwa n Münzwürfe. ⊗ soll dabei für ein mehrfaches kartesisches Produkt stehen, ganz, wie ∑ für eine mehrfache Summe steht. Wir haben also einfach ein Produktexperiment von Bernoulliexperimenten. Auf diesem Raum betrachten wir X, ” Zahl der u in 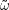∈ 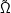“. Die Verteilung von X heißt Binomialverteilung (oder Bernoulli-Verteilung):

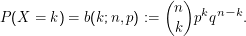
Das lässt sich so einsehen: Jedes Element des Ereignisses A=” genau k-mal u in 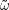“ hat die Wahrscheinlichkeit p^kq^n-k. Es bleibt die Frage nach der Kardinalität dieses Ereignisses. Effektiv ziehen wir k Positionen der u ohne Zurücklegen aus n Kugeln, wobei die Reihenfolge keine Rolle spielt, was unserem Modell Ω_III entspricht. Damit ist |A|= (n k)

Es gilt E(X) = np und Var(X) = npq. E(X) für n= 1 ist natürlich p, wegen der Linearität des Erwartungswerts summiert sich das einfach n Mal. Var(X) für n= 1 ist

hier addieren sich die individuellen Varianzen, weil die X alle unabhängig sind. Verteilungen dieser Art treten immer auf, wenn unabhängige, identisch verteilte Experimente (independent identically distributed, i.i.d.) hintereinander ausgeführt werden.

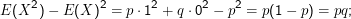
Normalverteilung

Die Standard-Normalverteilung ist definiert als

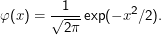
Es handelt sich hier um eine Dichte, x ist reell. Mit solchen Dichten können wir eigentlich nicht umgehen, weil unsere Wahrscheinlichkeitsräume und damit auch Zufallsvariablen immer diskret waren und das auch bleiben sollen. Wir ignorieren diese Probleme so gut wie möglich.

Diese ” Gaußkurve“ sieht so aus:

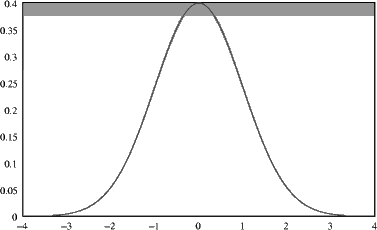
Es gilt der Zentrale Grenzwertsatz: Seien X_i, i= 1,…,n i.i.d. Zufallsvariable mit E(X_i) = 0 und Var(X_i) = 1. Sei S_n = 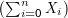∕ 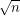. Dann gilt

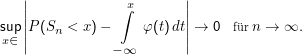
Der Beweis ist relativ schwierig. Die Einschränkung für die Zufallsvariablen ist nicht wichtig, man sie kann (fast) immer durch Einfühung einer neuen Zufallsvariablen erzwingen, etwa durch Subtraktion des Erwartungswerts und Division durch Standardabweichung. Damit besagt dieser Satz im Wesentlichen, dass alle Experimente, wenn ich sie nur oft genug hintereinander ausführe, schließlich auf normalverteilte Zufallsvariablen führen werden.

Vorsicht: Der Satz macht keine Aussage darüber, wie schnell das geht. Solange n ” klein“ ist (und ” klein“ kann durchaus noch drei Dezillionen sein), kann die tatsächliche Verteilung von der Normalverteilung beliebig abweichen.

Die Funktion ∫ _-∞^xφ(t)dt, die angibt, wie viel ” Wahrscheinlichkeit“ unterhalb von x liegt, heißt Verteilungsfunktion. Verteilungsfunktionen sind vor allem wichtig, wenn man mit kontinuierlichen Verteilungen arbeitet; die Verteilung (hier auch Dichte) ergibt sich als Ableitung der Verteilungsfunktion.

Standard-Normalverteilung heißt die oben vorgestellte Verteilung, weil sie Erwartungswert Null und Varianz 1 hat. Normalverteilungen zu beliebigen Erwartungswerten μ und Varianzen σ² werden durch die Funktionen

dargestellt.