11. Das schwache Gesetz der großen Zahlen

Leitfragen

Wie bekommt man eine Verbindung zwischen der Verteilung einer Zufallsvariablen und den Ergebnissen von Zufallsexperimenten hin?
Was ist der Unterschied zwischen einem Mittelwert und einem Erwartungswert?
Warum sind große Samples so wichtig?

Die tschebytschewsche Ungleichung für eine Zufallsvariable X lautet

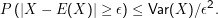
$P (|X - E (X )| ≥ ϵ) ≤ Var(X )∕ϵ2.$

Beweis: Sei Z= X-E(X), also einfach X, nur auf Erwartungswert Null getrimmt. Definiere neue Zufallsvariable Y mit

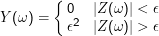
${ 0 |Z(ω )| < ϵ Y (ω ) = ϵ2 |Z(ω )| > ϵ$

Das sieht zunächst komisch aus, hat aber den Vorteil, dass wir einerseits sicher wissen, dass Y≤|Z|² (und das werden wir in der Abschätzung brauchen), wir aber den Erwartungswert von Y gut ausrechenen können (wir haben nämlich de facto ein Bernoulliexperiment). Konkret haben wir mit diesem Trick erreicht:

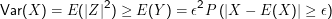
$2 2 Var(X ) = E (|Z | ) ≥ E (Y ) = ϵ P (|X - E(X )| ≥ ϵ)$

Große Abweichungen vom Erwartungswert werden um so unwahrscheinlicher, je kleiner die Varianz ist.

Wichtige Folge: Das ” schwache Gesetz der großen Zahlen“.

Seien X₁,…,X_n i.i.d. Zufallsvariable mit beschränkter Varianz. Sei H_n = 1∕n∑ _i=1ⁿX_i. Es gilt mit ϵ >0 und einer Konstanten M:

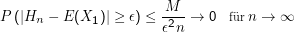
$-M-- P (|Hn - E (X1 )| ≥ ϵ) ≤ ϵ2n → 0 f¨ur n → ∞$

Beweis: Wegen der Linearität des Erwartungswerts und unserer i.i.d.-Annahme ist E(H_n) = E(X₁). Außerdem ist

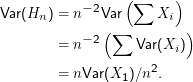
$( ∑ ) Var(Hn ) = n - 2Var Xi (∑ ) = n - 2 Var(X ) i = nVar (X )∕n2. 1$

Mit Tschebytschew ist nun

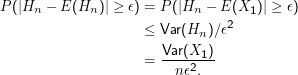
$P (|Hn - E (Hn )| ≥ ϵ) = P (|Hn - E (X1 )| ≥ ϵ) 2 ≤ Var(Hn )∕ϵ Var(X1 ) = --nϵ2.---$

Das ist mit M= Var(X₁) der eine Teil der Behauptung. Der andere folgt, weil M und ϵ konstant sind und 1∕n für große n gegen Null geht.

Die Aussage ist also, dass bei vielen identischen Experimenten die Wahrscheinlichkeit, dass die Summe der Ergebnisse geteilt durch die Zahl der Ergebnisse (der Mittelwert einer Meßreihe) weit vom Erwartungswert abliegt, beliebig klein wird.

Tatsächlich ist die Abschätzung aus dem Gesetz der großen Zahlen bzw. aus der tschebytschewschen Ungleichung in aller Regel zu pessimistisch, gibt also relativ große Grenzen für die Wahrscheinlichkeit an, die normalerweise bei weitem nicht erreicht werden. Der Grund dafür ist die große Allgemeinheit von Tschebytschew, der sozusagen noch für die übelsten Verteilungen (etwa mit zwei ganz spitzen Maxima) gelten muss, während die meisten Verteilungen, denen man im Alltag so begegnet, viel netter sind. Wie man ” bessere“ (man sagt auch gern ” schärfere“) Abschätzungen bekommt, werden wir noch sehen.

Diese Formel liefert den Zusammenhang zwischen experimentell ermittelbaren relativen Häufigkeiten und einem Parameter der Verteilung.

Beispiel: Ω seien die Wörter eines deutschen Textes, die Zufallsvariable ist die Länge eines ” zufällig“ gezogenen Worts. Es kann dann sein:

X₁	X₂	X₃	X₄	X₅	X₆	X₇	X₈	X₉	X₁₀
11	4	13	4	7	8	9	6	6	6

Sei von irgendwo bekannt, dass Var(X) = 12 (also die Wortlänge in irgendeinem Sinn typisch um √ ---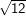
12 ≈3.5 vom Erwartungswert abweicht).

Es ist H₄ = 8, die Wahrscheinlichkeit, dass die tatsächliche mittlere Wortlänge des Deutschen um zwei oder mehr (also ϵ= 2) von 8 abweicht, also höchstens 12∕2²∕4 = 0.75 (die Abschätzung ist nicht sehr gut… ). Die Wahrscheinlichkeit, dass sie um 5 oder mehr von 8 abweicht, ist höchstens 12∕5²∕4 = 0.12

Es ist H₁₀ = 7.4. Abweichung um 5 oder mehr mit höchstens 0.048, Abweichung um 1 oder mehr mit höchstens 1.2.

Übungen zu diesem Abschnitt

Ihr solltet euch wenigstens an den rötlich unterlegten Aufgaben versuchen

(1)

Im Anhang dieser Seite befindet sich ein Programm, dem ihr Erwartungswert und Varianz einer Zufallsvariable sowie eine Zahl n der Experimente vorgeben könnt und das dann einige Male diese Zahl gerade n Werte der Zufallszahlen zieht. Das Programm rechnet dann H_n und seine Abweichung vom Erwartungswert aus und gibt am Schluss die kumulierten relativen Häufigkeiten bestimmter Abweichungen aus. Ein Beispiellauf:

examples> python tschegame.py 1 20 400

Relative Häufigkeit |H_n-E(X)|>=3: 0.005000
Relative Häufigkeit |H_n-E(X)|>=2: 0.055000
Relative Häufigkeit |H_n-E(X)|>=1: 0.330000
Relative Häufigkeit |H_n-E(X)|>=0: 1.000000

Seht euch das Programm an und macht euch klar, dass es letztlich versucht, das schwache Gesetz der großen Zahlen (sGgZ) experimentell zu prüfen.

Führt diese Prüfung durch, d.h. vergleicht die Vorhersagen aus dem sGgZ mit dem, was das Programm findet. Tut das für verschiedene Werte des Erwartungswerts (im ersten Kommandozeilenargument), der Varianz (im zweiten) und dem n aus dem H_n (im dritten) – für diesen Vergleich müsst ihr schon annehmen, dass die relativen Häufigkeiten, die das Programm ausgibt, tatsächlich gute Schätzungen für die Wahrscheinlichkeiten aus dem sGgZ sind – wenn ihr wollt, könnt ihr mit dem sGgZ selbst schon nachsehen, wie groß die Wahrscheinlichkeit ist, dass das Programm sich arg irrt…

Was stellt ihr fest? Warum ist das kein Widerspruch zum sGgZ? Könnt ihr euch vorstellen, wie bei so einer Abschätzung von Wahrscheinlichkeiten anch oben der Begriff ” scharf“ zu verstehen wäre?

(2)

Wenn wir glauben, die Varianz der Zufallsvariable X ” Länge eines Wortes“ sei im Deutschen tatsächlich 12: Wie viele Wörter muss ich ansehen, damit mir schon das Gesetz der großen Zahl garantiert, dass meine E(X)-Schätzung nur mit, sagen wir, 10%, 5%, 1% um 1, 0.5, 0.1 (oder natürlich jeweils mehr) danebenliegt?

(3)

Über welchem Wahrscheinlichkeitsraum sind unsere H_n aus dem Beweis des schwachen Gesetzes der großen Zahl eine Zufallsvariable?

Dateien zu diesem Abschnitt

chegame.py -- Ein Programm, um via Experiment Vertrauen zum schwachen Gesetz der großen Zahlen zu gewinnen

Zurück: Häufig auftretende Verteilungen

Inhalt

Weiter: Schätztheorie I

Index

Markus Demleitner