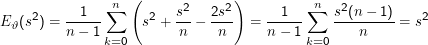12. Schätztheorie I

Mit dem schwachen Gesetz der großen Zahlen kann man offenbar Erwartungswerte aus Beobachtungen ” kontrolliert schätzen“. Geht das auch für Varianz oder andere Parameter?

Dafür Schätztheorie mit

• einem Stichprobenraum Ω
• einer Familie von Verteilungen {P_ϑ|ϑ∈Θ}
• einem zu schätzenden Parameter ϑ

In der Schätztheorie ist Ω im Allgemeinen ein Produkt aus n unabhängigen Einzelexperimenten, während ϑ ein Parameter der Verteilung der Einzelexperimente ist.

Beispiel: Schätze die Wahrscheinlichkeit, dass ein zufällig gezogenes Wort länger als 5 Zeichen ist. Der Stichprobenraum ist {0,1}ⁿ (1 für ” Wort länger als 5“). Wir haben ein Bernoulli-Experiment, unsere Familie von W-Maßen ist also

Wir haben dabei ganz flott eine Zufallsvariable X eingeführt, die Zahl der Einsen in ω; x ist ihr Wert beim vorliegenden Experiment.

Wir wollen p schätzen, also ist ϑ= p.

Das Ganze ließe sich noch etwas verallgemeinern durch Einführung einer Funktion g:Θ →Y, so dass man direkt nicht nur den Parameter ϑ, sondern gleich funktional davon abhängige Größen schätzen kann. Das allerdings verkompliziert die Notation und bringt wenig tiefere Einsicht, weshalb wir hier darauf verzichten.

Der Maximum-Likelihood-Schätzer für ϑ ist eine Abbildung 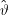:Ω →Θ, so dass die Likelihood-Funktion L_ω(ϑ) = P_ϑ(ω) für (ω) maximal wird.

Generell heißt jede Abbildung 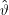: Ω →Θ Schätzer (estimator) von ϑ– darin sind natürlich auch Schätzer, die völligen Quatsch schätzen.

Noch einmal: ϑ ist einfach ein Parameter, 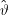:Ω →Θ eine Funktion, 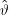(ω) der konkrete Schätzwert, der aus der Beobachtung der Stichprobe ω folgt, also das ϑ, das wir als in irgendeinem Sinne ” besten“ Parameter zur Erkärung der Beobachtung ansehen.

Der Maximum-Likelihood-Schätzer ist so gebaut, dass er den Parameter ϑ= ϑ₀ wählt, für den bei der konkreten Beobachtung ω die Ungleichung P_ϑ0(ω) ≥P_ϑ(ω) für alle ϑ∈Θ gilt – man maximiert also die Wahrscheinlichkeit für das Auftreten von ω durch Wahl derjenigen Verteilung, in der ω gerade die höchste Wahrscheinlichkeit hat.

Das ist absolut nicht zwingend – es wäre etwa auch denkbar, dass wir ein paar ” benachbarte“ P_ϑ(ω) zusammenzählen und diese Größe maximieren. Oder wir misstrauen unserer Beobachtung in irgendeiner systematischen Weise und bauen dieses Misstrauen in unseren Schätzer ein.

Im Beispiel ist die Likelihood-Funktion

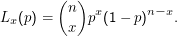
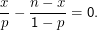
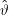Das Maximum dieser Funktion bestimmt man am Besten nach Logarithmierung (dann werden die hässlich abzuleitenden Produkte zu einfach abzuleitenden Summen, Maxima bleiben aber Maxima). Wir müssen sehen, wo die Ableitung nach p Null wird. Also: Eine Lösung davon ist p= x∕n. In der Tat ist dort ein Maximum, also ist der ML-Schätzer für unser Problem (ω) = x∕n mit x der Zahl der Wörter länger als fünf und n der Zahl der Wörter insgesamt.

Das hätte einem natürlich schon der gesunde Menschenverstand gesagt, in der Realität sind die Probleme aber nicht so einfach, und häufig versagt der gesunde Menschenverstand.

Für eine Zufallsvariable T:Ω →ℝ ist E_ϑ(T) = ∑ _ω∈ΩT(ω)P_ϑ(ω) der Erwartungswert von T bezüglich P_ϑ. Ein Schätzer heißt erwartungstreu (unbiased), wenn

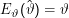
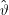für alle ϑ. Der Bias von ist

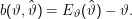
Was bedeutet Erwartungstreue? So, wie wir unsere Schätztheorie aufgezogen haben, behaupten wir, es gebe ein ” wahres“ ϑ, das von einem konkreten System realisiert wird. Die Zufallsvariable, mit der wir schätzen, ist dann eben gemäß ϑ verteilt. In unserem Beispiel oben wird ein Schätzer nun zu jedem möglichen x∈{0,1,…n} ein (x) = x∕n liefern, also mitnichten jedes Mal das wahre ϑ– wenns so einfach wäre, bräuchten wir keine Schätztheorie.

Ein erwartungstreuer Schätzer 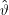liefert aber im Mittel das richtige ϑ. Warum? Wenn wir das Experiment ganz oft (sagen wir, N Mal) mit unabhängigen Samples, die alle gemäß ϑ verteilt sind, wiederholen, sollte nach dem Gesetz der großen Zahlen mit 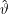als Zufallsvariable

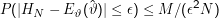
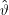gelten, H_N = 1∕N ∑ _i=1^N(x_i) also schließlich fast immer sehr nah an E_ϑ(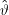) liegen. H_N ist aber gerade die Schätzung, die wir aus einer langen Versuchsreihe ableiten, während E(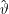) bei einem erwartungstreuen Schätzer gerade ϑ ist – anders gesagt: wenn wir so lange experimentieren, dass wir jedes x aus dem Wertebereich von X tatsächlich mit NP_ϑ(X= x) Mal beobachten, liefert ein erwartungstreuer Schätzer wirklich den wahren Wert.

Ist unser ML-Schätzer erwartungstreu? Rechnen wir nach:

weil der zu berechnende Term (in der Summe steht einfach der Schätzer x∕n und die Verteilung P_ϑ) gerade der Erwartungswert der Bernoulli-verteilten Zufallsvariablen X= x ist, den wir oben zu np berechnet hatten. Demnach ist unser Schätzer erwartungstreu.

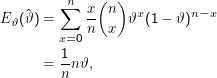
Haben wir einen nicht-erwartungstreuen Schätzer, ziehen wir offenbar etwas aus den Daten, das zunächst nicht drinsteht – es weicht eben gerade um den Bias davon ab. Hat sowas überhaupt einen Sinn? Ja, denn erwartungstreue Schätzer sind zwar dann gut, wenn man Ω oder analog den Wertebereich von X im erwähnten Sinn ” ausschöpfen“ kann. Wenn wir aber wissen, dass das garantiert nicht passiert, ist auch klar, dass ein erwartungstreuer Schätzer garantiert ein falsches Ergebnis liefert.

Wir könnten beispielsweise die Wahrscheinlichkeiten schätzen, mit denen bestimmte Wörter auf auf das Wort ” im“ folgen: im Haus, im Hörsaal, im Neckar usw. Wir wissen, dass es auch mal ” im Rhein“ sein kann, selbst wenn wir das nicht sehen – nicht-erwartungstreue (und nicht-ML) Schätzer erlauben uns, für sowas Platz zu reservieren. In diesem Fall haben wir ein (begründetes) ” Vorurteil“ (eben ein bias) über die Qualität unserer Daten, und das sollten wir besser in unseren Schätzer einbauen, wenn wir brauchbare Ergebnisse erhalten wollen.

Der bias hängt übrigens offenbar von ϑ ab. Das ist auch gut so, denn es mag durchaus sein, dass man z.B. für große ϑ einen kleinen Bias haben möchte und für kleine einen größeren. Wenn wir im obigen Beispiel bei 1000 Bigrammen mit ” im“ sagen wir 30 Mal ”im Haus“ finden und nur 1 Mal ” im Neckar“, würden wir 30/1000 wohl als eine ganz brauchbare Schätzung für die Wahrscheinlichkeit von ” im Haus“ ansehen, während wir nicht sicher sein können, ob ” im Neckar“ nicht in Wirklichkeit sehr selten sein sollte, wir aber zufällig einen Text erwischt haben, der über Heidelberg redet (was auch schon andeutet, dass der Stichprobenraum bei Schätzproblemen eminent wichtig ist – P(” im Neckar“) hat, wenn der Stichprobenraum ” alle möglichen Texte über Heidelberg“ heißt, einen ganz anderen Wert als über dem Stichprobenraum ” Texte, die sich mit Wüsten beschäftigen“). Entsprechend würden wir das 1/1000 von ” im Neckar“ wohl deutlich stärker bestrafen als das 30/1000 von ” im Haus“.

Ein populärer nicht-erwartungstreuer Schätzer für Häufigkeiten dieser Art ist Expected Likelihood Expectation (ELE, auch Jeffreys-Perks-Gesetz, hier für Bigramme formuliert):

Darin ist |w₁w₂| die absolute Häufigkeit des Bigramms w₁w₂, N die Zahl der beobachteten Bigramme (quasi der word tokens) und B die Zahl der verschiedenen möglichen Bigramme (also quasi der word types) – es ist eingestandenermaßen nicht immer offensichtlich, wie viele das wohl sein werden.

So, wie das gemacht ist, wird also im Zähler ein bisschen was addiert, im Nenner ein bisschen mehr, so dass die Wahrscheinlichkeiten kleiner werden, und zwar um so mehr, je kleiner die relative Frequenz von w₁w₂ ist. Nur haben eben auch ungesehene word types eine finite Wahrscheinlichkeit (nämlich 1∕(2N+ B)). Diese Formel lässt sich übrigens sogar begründen als in irgendeinem Sinn optimale Mischung zwischen einer ML-Schätzung und einer Bayesianischen Schätzung mit gleichverteiltem Prior (dazu später mehr).

Der mittlere quadratische Fehler eines Schätzers ist

Den zweiten Teil der Gleichung sieht man so ein:

Das kann man quadrieren und ausmultiplizieren. Danach steht unter Ausnutzung der Linearität des Erwartungswerts das Ergebnis fast schon da – problematisch bleibt nur das gemischte Glied, das nach Ausmulitplizieren lautet.

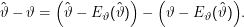
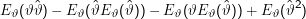
Nun sind die Erwartungswerte in den Klammern Konstanten und ziehen sich vor die Klammer, also heben sich die Terme 2 und 4 weg. Außerdem ist ϑ für die Berechnung von E_ϑ ebenfalls konstant und kann aus dem Erwartungswert herausgezogen werden, also heben sich auch die Terme 1 und 3 weg.

Ein Streben nach möglichst kleinen mittleren quadratischen Fehlern ist übrigens ein weiterer Grund, von der Erwartungstreue Abstand zu nehmen. Am Ende des Tages interessiert man sich bei einem Schätzer eben doch eher dafür, wie sehr er sich bei realen Experimenten verschätzt als dafür, ob er, wenn man Ω koplett abgrasen würde und alle Ergebnisse mit den nach ihren Wahrscheinlichkeiten zu erwartenden Frequenzen erhalten hat, das wahre und endgültige ϑ liefern würde – eben weil dies meist unmöglich ist. Auf der letzten Folie zum Good-Turing-Schätzer werden beispielsweise wir einen Graphen sehen, der zeigt, dass für ein recht typisches Problem der nicht-erwartungstreue Good-Turing-Schätzer durchweg erheblich geringere mittlere quadratische Fehler aufweist.

Ein erwartungstreuer Schätzer für den Erwartungswert einer Zufallsvariablen X, die in n unabhängingen Experimenten mit Ausgängen X_k beobachtet wird, ist der Mittelwert

für das Quadrat ihrer Standardabweichung s² Warum sind diese Schätzer erwartungstreu? Es ist Wir brauchen dabei weder ϑ noch die Familien P_ϑ∈Θ festzulegen – die Formel gilt unabhängig von der konkreten Modellierung, interessant ist nur der Erwartungswert. Dies ist einer der Fälle, in denen man dringend nicht die Parameter der Verteilungen (weil wir gar keine Verteilungen annehmen), sondern stattdessen direkt eine Funktion des Parameters (nämlich den Erwartungswert) schätzen möchte. Dieses formale Detail soll uns jetzt nicht stören.

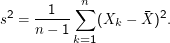
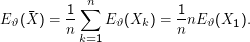
Das n-1 im Zähler des Schätzers für s² wird häufig als mystisch deklariert. In der Tat führt diese Wahl aber zu einem erwartungstreuen Schätzer:

Wir rechnen die Summanden aus und bezeichnen μ= E_ϑ(X_i):

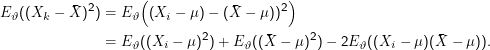
Der erste Summand in diesem Ausdruck ist per definitionem s². Der zweite Summand lässt sich folgendermaßen berechnen:

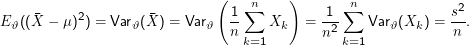
Bleibt der letzte Summand. Es ist

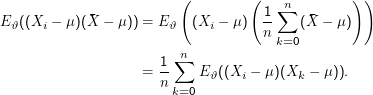
Der Erwartungswert in der letzten Zeile ist gerade die Kovarianz. Da die verschiedenen Experimente unkorreliert sind, ist diese Null, wenn i≠k. Also schnurrt die Summe zusammen auf den Term E_ϑ(X_i -μ)² und damit auf s² .

Zusammen ist