Wie genau ist jetzt so ein Schätzer? Das weiß man nie, weil er durch seine Stochastizität immer beliebig daneben liegen kann. Man kann aber eine Wahrscheinlichkeit dafür angeben, dass ein Intervall das ” wahre“ ϑ enthält.
Um das zu untersuchen, wollen wir als Versuchsergebnis eine Zufallsvariable X mit Werten x∈X annehmen. Natürlich funktioniert das auch ohne Zufallsvariablen und direkt auf Ω, aber wir werden in der Regel nicht direkt Versuchsergebnisse, sondern von ihnen abhängige Zufallsvariablen untersuchen.
Wir geben eine Familie von Teilmengen {C(x) ⊂Θ|x∈X} an, so dass für alle ϑ∈Θ
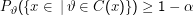
Seht euch diese Gleichung genau an – sie ist letztlich der Schlüssel zum Verständnis frequentistischer Schätztheorie. Das Argument von P ϑ ist eine Menge, und der senkrechte Strich markiert keine bedingte Wahrscheinlichkeit, sondern ein ” mit der Eigenschaft“ in der Menge. Intuitiv würde man von einem Schätzer gerne haben, dass er etwas wie P(ϑ∈C(x)) ≥1 -α sagt, dass also die Wahrscheinlichkeit, dass ϑ im Konfidenzintervall ist, größer als eine Schranke ist – damit könnten wir den Messfehler einer bestimmten Messung x kontrollieren.
Die Art, wie wir die Schätztheorie hier aufgezogen haben, lässt das aber nicht zu, weil ϑ keine Zufallsvariable ist (Nebenbei: 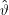 wäre
eine Z.V., über der man Verteilungen haben kann – aber hier liefert der Schätzer ja stattdessen die C(x) als Z.V.). Deshalb ist
ϑ∈C(x) bei gegebenem x ist kein Ereignis, sondern einfach wahr oder falsch.
wäre
eine Z.V., über der man Verteilungen haben kann – aber hier liefert der Schätzer ja stattdessen die C(x) als Z.V.). Deshalb ist
ϑ∈C(x) bei gegebenem x ist kein Ereignis, sondern einfach wahr oder falsch.
Unser Umweg über die Menge aller x, die für ein bestimmtes ϑ zusammen eine bestimmte Wahrscheinlichkeitsmasse sammeln, erlaubt uns das Rumdrücken um dieses konstruktionsbedingte Problem, allerdings um den Preis einer weniger intuitiven Interpretation.
Was wir kontrollieren, ist die Irrtumswahrscheinlichkeit bei einem bestimmten Modell. Ist nämlich das System, das wir beobachten, eine
Realisierung des durch 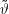 beschriebenen Modells, und beobachten wir das oft genug, werden nur 5% (für α= 0.05) der Messwerte
außerhalb des Konfidenzbereichs liegen. Leider ist damit keine Aussage möglich, wie wahrscheinlich Fehler für ein gegebenes x sind.
Eine Möglichkeit, diesem Phänomen etwas nachzugehen, ist die Beobachtung der Wahrscheinlichkeitsmasse in den unten definierten
A(ϑ) – da ist einfach alles möglich.
beschriebenen Modells, und beobachten wir das oft genug, werden nur 5% (für α= 0.05) der Messwerte
außerhalb des Konfidenzbereichs liegen. Leider ist damit keine Aussage möglich, wie wahrscheinlich Fehler für ein gegebenes x sind.
Eine Möglichkeit, diesem Phänomen etwas nachzugehen, ist die Beobachtung der Wahrscheinlichkeitsmasse in den unten definierten
A(ϑ) – da ist einfach alles möglich.
Eine – im statistischen Mainstream allerdings unpopuläre – Alternative, die eine intuitive Interpretation liefert, werden wir später als Belief Intervals kennenlernen.
Woher kommen die C(x)? Entweder aus Tschebytschew, der aber meistens zu große Intervalle liefert, weil er die Verteilung nicht kennt. Ansonsten existieren viele ” vorberechnete“ Schätzer, für die Konfidenzintervalle bekannt sind. Im Allgemeinen ist das Verfahren aufwändig.
Idee: Gebe
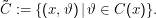
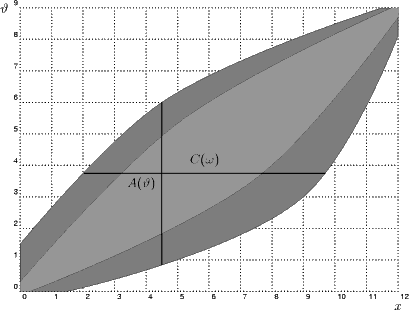
Die Figur oben zeigt zwei mögliche 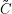 , wobei der hellere Part zwar kleinere Signifikanzintervalle liefert, diese aber weniger signifikant
sind (nämlich weniger Wahrscheinlichkeit auf sich vereinen.)
, wobei der hellere Part zwar kleinere Signifikanzintervalle liefert, diese aber weniger signifikant
sind (nämlich weniger Wahrscheinlichkeit auf sich vereinen.)
Beachtet, dass ϑ hier irgendwelche Werte zwischen 0 und 9 annehmen kann. Das ist komplett in Ordnung, wir haben keine Aussagen darüber gemacht, was Θ eigentlich sei (auch wenn eine der Standardanwendungen die Schätzung des p von Binomialverteilungen und damit Θ = [0,1] ist). Was der Parameter hier bedeutet, verrate ich natürlich nicht.
Konkret lassen sich die A(ϑ) wie folgt definieren:
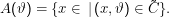
Die A(ϑ) enthalten also die x, die für ein gegebenes Signifikationniveau auf ϑ führen können.
Wir konstruieren die A(ϑ) so, dass
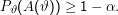
Daraus ergeben sich umgekehrt die C(x).
Ein diskretes Beispiel. Wir wollen schätzen, wie groß die Wahrscheinlichkeit ist, dass auf das Wort ” Louis“ das Wort ” Philippe“ folgt und werden versuchen, das aus dem Text ” Eighteenth Brumaire of Louis Bonaparte“ (Project Gutenberg, mar1810.txt) zu schätzen.
Wenn wir zunächst den Stichprobenraum 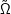 , ” Bigramme im Englischen“ betrachten und mit w1, w2 das erste bzw. zweite Wort eines
Bigramms bezeichnen, können wir die Ereignisse A= {w2 = Phillipe} und B= {w1 = Louis} definieren. Wir interessieren wir uns
für die Größe p:= P(A|B). Der ML-Schätzer für diese Größe ist einfach:
, ” Bigramme im Englischen“ betrachten und mit w1, w2 das erste bzw. zweite Wort eines
Bigramms bezeichnen, können wir die Ereignisse A= {w2 = Phillipe} und B= {w1 = Louis} definieren. Wir interessieren wir uns
für die Größe p:= P(A|B). Der ML-Schätzer für diese Größe ist einfach:
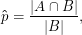
Um unser Schätzproblem zu formulieren, nehmen wir jetzt alle möglichen (englischen) Texte als Ω. Wir betrachten die Zufallsvariable X= |A∩B|. Als Modelle für die Verteilungen dieses X nehmen wir Bernoulli-Verteilungen an:
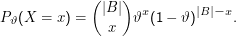
Als Θ würde man normalerweise [0,1] verwenden; wir wollen es aber diskret haben und setzen Θ = {0.1,0.3,0.5,0.7,0.9}.
Durch simples Ausrechnen von Pϑ(x) für die verschiedenen Elemente von Θ und x errechnet sich folgendes Tableau:
| x ϑ | 0-4 | 5-9 | 10-14 | 15-19 | 20-24 | 25-29 | 30-34 | 35-40 | 40-44 | |
| 0.1 | ♡0.547 | ♡0.443 | 0.010 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 0.3 | 0.001 | ♡0.108 | ♡0.563 | ♡0.306 | 0.022 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 0.5 | 0.000 | 0.000 | 0.011 | ♡0.214 | ♡0.549 | ♡0.214 | 0.011 | 0.000 | 0.000 | |
| 0.7 | 0.000 | 0.000 | 0.000 | 0.000 | 0.022 | ♡0.306 | ♡0.563 | ♡0.108 | 0.001 | |
| 0.9 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.010 | ♡0.443 | ♡0.547 | |
| C(x) | {.1} | {.1,.3} | {.3} | {.3,.5} | {.5} | {.5,.7} | {.7} | {.7,.9} | {.9} |
Dabei wurden, beginnend bei den größten, immer alle Werte in einer Zeile mit Herzlein markiert, bis die Summe der geherzten Wahrscheinlichkeiten über 0.95 lag – die in einer Zeile geherzten x bilden dann zusammen die A(ϑ) zum Signifikanzniveau 0.05. Dann lassen sich in den Spalten die C(x) ablesen. Damit weiß ich beispielsweise, dass bei 19 beobachteten Phillipes die Menge {0.3,0.5} nur mit einer Wahrscheinlichkeit von 0.05 das tatsächliche ϑ nicht enthält.
Ein anderes Problem ist natürlich, dass der Text, aus dem wir diese Schätzung abgeleitet haben, eher nicht repräsentativ für Texte ist – ein schneller Blick auf google lehrt, dass am Netz etwa 11 Millionen Bigramme mit Louis existieren, aber nur etwa 67 000 auch mit Philippe weitergehen. Solche Fehler werden wir bald als ” Fehler dritter Art“ kennen lernen.
Natürlich macht in Wirklichkeit niemand solche Rechnungen (oder jedenfalls nur im äußersten Notfall). Wenn man in der Praxis Schätzer verwendet, ignoriert man entweder einfach den Umstand, dass die Schätzungen fehlerbehaftet sind (das machen leider viel zu viele Leute, auch wenn es durchaus genug Anwendungen gibt, bei denen das legitim ist), oder man bekommt mit der Formel für den Schätzer eine Formel für die Größe der Konfidenzbereiche mit.
Um eine ganz grobe Schätzung der Größe der Konfidenzbereiche zu bekommen, reicht es häufig auch, aus den rohen
Zählungen N schlicht N-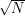 und N+
und N+ 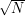 zu berechnen und diese durch die jeweilige Maschinerie zu ziehen.
Das Ergebnis könnte mit Glück der so genannte 1-σ-Konfidenzbereich sein, der einem Schätzer zum Niveau 0.33
entspricht. Dass diese Magie häufig funktioniert, liegt am oben erwähnten zentralen Grenzwertsatz. Da wir uns mit
diesem nicht näher auseinandergesetzt haben, wollen wir auch dieser Faustregel nicht näher unter die Haube gucken.
zu berechnen und diese durch die jeweilige Maschinerie zu ziehen.
Das Ergebnis könnte mit Glück der so genannte 1-σ-Konfidenzbereich sein, der einem Schätzer zum Niveau 0.33
entspricht. Dass diese Magie häufig funktioniert, liegt am oben erwähnten zentralen Grenzwertsatz. Da wir uns mit
diesem nicht näher auseinandergesetzt haben, wollen wir auch dieser Faustregel nicht näher unter die Haube gucken.