ML-Schätzer sind notorisch schlecht für Sprachdaten, vor allem, weil nicht beobachtete Phänomene automatisch Wahrscheinlichkeit Null bekommen und beobachtete Phänomene überschätzt werden.
Wir diskutieren die Alternativen am Beispiel des Wörterzählens. Natürlich würde das ganz analog mit n-grammen oder was immer gehen.
Ein einfacher Trick ist adding one. Dabei berechnet man

Dabei ist N die Zahl der Wörter (word tokens) im Korpus, |wi| die Häufigkeit des betrachteten Wortes und B die Anzahl der word types (die ich hier mal ” Spezies“ nennen möchte, weil der Schätzer natürlich für alles mögliche funktioniert), die wir erwarten. Im Beispiel ist das schon etwas schwierig, denn die Anzahl verschiedener Wörter in einer Sprache ist keine zugängliche Größe (auch wenn ich argumentieren würde, dass sie finit ist). Einfacher ist das z.B. mit n-grammen über einer bekannten Anzahl grammatischer Kategorien o.ä.
Der Effekt ist, dass Wahrscheinlichkeit für die unbeobachteten Spezies reserviert wird. Beobachten wir etwa nur n < B verschiedene Wörter, so ist die Summe der Wahrscheinlichkeiten
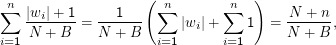
Obwohl diese Variation des oben erwähnten ELE-Schätzers nicht so beliebig ist, wie es vielleicht scheinen mag (es ist das Ergebnis, wenn man nach Bayes schätzt und annimmt, dass alle Spezies a priori gleich wahrscheinlich sind), sind die Ergebnisse meist schlecht, zumal für beobachtete Spezies oft schlechter als ML-Schätzungen.
Besser ist der Good-Turing-Schätzer, der für typische Anwendungen der Computerlinguistik einen guten Kompromiss aus bias und mittlerem quadratischen Fehler bietet.
Die Situation: Wir haben s Spezies, die unabhängig voneinander mit Wahrscheinlichkeiten pi, i= 1,…,s beobachtet werden. Die Stichprobe besteht aus tatsächlich beobachteten Frequenzen r1,…,rs mit N= ∑ i=1sri.
Wir disktuieren hier ” Spezies“, weil, wie gesagt, bei weitem nicht nur Word Types in Frage kommen.
Grundidee
Wir fragen zunächst nach der Anzahl der gerade r Mal auftretenden Spezies, nr. Für diese lässt sich zeigen:
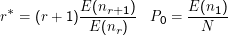
Der Beweis dieses Theorems ist zu aufwändig, als dass ich ihn hier breit diskutieren wollte – er braucht aber eigentlich keine schweren Geschütze. Ausgangspunkt ist dabei, dass die beobachteten Frequenzen mit pi Bernoulli-verteilt sind. Damit lässt sich E(nr) hinschreiben. Mit einigen Umformungen auch des Binomialkoeffizienten lässt sich der Beweis führen.
Übrigens verwende ich hier Sampsons Notation. Wir haben Schätzer bisher immer mit einem Zirkumflex geschrieben, die Größe oben
wäre dann also etwas wie  , also ein Schätzer für die ” wahre“ Häufigkeit.
, also ein Schätzer für die ” wahre“ Häufigkeit.
Für E(nr) könnten wir unsere Beobachtungen einsetzen. Für kleine r ist das auch gut (weil nr groß ist); für große r klappt das nicht mehr gut, weil nr klein oder gar Null wird.
Es ist die Lösung dieses Problems, das die Anwendung von Good-Turing im allgemeinen Rahmen etwas schwierig macht. Für praktisch alle interessanten Anwendungen in der Computerlinguistik gibt es aber eine recht einfache Lösung: Wir fitten Zipf’s Law auf die beobachtete Verteilung und schätzen E(nr) für kleine nr aus dem Fit. Das resultierende Verfahren wird meistens unter einem Titel wie Simplified Good-Turing (SGT) vorgestellt. Mehr darüber ist in dem sehr empfehlenswerten Buch ” Empirical Linguistics“ von Geoffrey Sampson zu erfahren.
Was ist ein Fit? Wenn man Beobachtungsdaten hat und vermutet, dass sie eigentlich durch eine Funktion einer bestimmten Form beschrieben werden sollten, versucht man, die Parameter der Funktion so zu bestimmen, dass sie die Beobachtung ” möglichst gut“ beschreiben, dass also ein irgendwie definierter Fehler möglichst klein wird. Wie wir das hier machen, sehen wir unten.