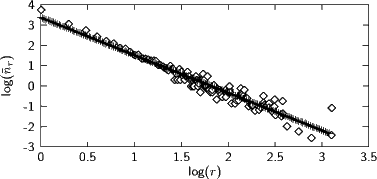
Zipf’s law spricht von Wortfrequenzen r und Frequenzen von Wortfrequenzen nr. Uns interessiert also z.B. die Information, dass es n20 = 4 Spezies gibt, die r= 20 Mal im Korpus auftreten. Außerdem behauptet Zipf’s Law, dass eine lineare Beziehung zwischen den Logarithmen von r und nr gibt.
Plot von log nr gegen log r für einen kleinen Korpus:
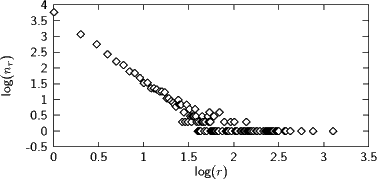
Es ist wichtig, diesen Plot zu verstehen, zumal er anders orientiert ist als die, die üblicherweise als Illustration für Zipf’s Law verwendet werden: Ganz links stehen die Spezies mit r= 1, also Wörter, die nur ein Mal vorkommen. Davon gibt es hier etwa 103.7. Dann gehen wir weiter zu Spezies mit zwei Vertretern usf. Rechts stehen demgegenüber die Spezies mit vielen Vertretern. Dabei gibt es zu jeder Frequenz r nur eine Spezies, log(nr) = 0.
Während man bei den niedrigfrequenten Wörtern Zipf’s Law recht gut realisiert sieht, ist das bei den hochfrequenten Wörtern nicht mehr so. Das liegt daran, dass es mehr oder minder Zufall ist, ob ” ist“ gerade 2104 Mal vorkommt oder doch 2105 Mal. Wir müssten eigentlich den Beitrag von ” ist“ zu n2104 für etliche der benachbarten nr ” verschmieren“, die Kurve also glätten.
1. Schritt: Glätten der beobachteten Verteilung
Wir behaupten, dass für große r die zugehörigen nr-Werte reduziert werden müssen. Eine gute Methode dazu ist, das nr gleichmäßig über die ” leeren“ r in der Nachbarschaft zu verteilen.
Konkret: Wir beobachten F Frequenzen ri, i= 1,…,F. Für große ri werden ri-1 und ri+1 in der Regel ziemlich weit von ri abliegen (z.B. r= 586, daneben r= 422 und r= 768, alle mit nr = 1 – die betreffenden Spezies sind hier ” in“, ” das“, und ” und“). Wenn wir das n586 = 1 über die ganze Nachbarschaft jeweils bis zur Hälfte des benachbarten r verschmieren. Die Größe dieser Nachbarschaft ist l= (768 -422)∕2, statt n586 nehmen wir also n586 ∕l.
Allgemein glätten wir, indem wir 
r = 2nr∕(r+ -r-) setzen, wobei r+ der nächsthöhere beobachtete r-Wert ist und r- der
nächstniedrigere. Bei r= 1 setzen wir r- = 0, beim höchsten Wert für r setzen wir r+ auf r+ (r-r-) (wir erweitern die
Nachbarschaft symmetrisch).
Das Ergebnis ist, dass sich nr-Werte gar nicht ändern, wenn wir sowohl für r-1 als auch für r+ 1 Spezies haben, dass sie aber um so stärker reduziert werden, je weiter der Abstand zwischen zwei ” besetzten“ r wird.
Das Ergebnis sieht dann so aus:
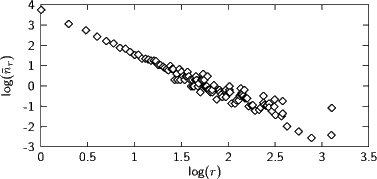
Das ist offenbar eine erhebliche Verbesserung gegenüber den rohen Daten. Vor allem die oberste Frequenz reißt aber etwas aus. Das ist ein Artefakt des Umstandes, dass die beiden häufigsten Wörter ” die“ und ” der“ mit r= 1269 und r= 1281 eigentlich viel zu nahe beieinanderliegen – das nächsthäufige Wort bei uns ist ” und“ mit r= 768. Solche Dinge passieren, und Schätzer müssen damit fertig werden (” robust sein“).
2. Schritt: Lineare Regression
Zipf’s Law behauptet, dass wir hier eine Gerade durchlegen können. Dazu dient die lineare Regression, ein mathematisches Verfahren,
das die ” beste“ Gerade ax+ b durch die beobachteten Daten (log r,log 
r) findet.
Dazu minimiert man den quadratischen Fehler der geschätzten Gerade gegenüber den gegebenen Punkten,∑
r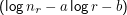
2,
d.h. sorgt dafür, dass die Ableitung dieser Größe Null wird. Das Ergebnis ist ein 2 ×2-Gleichungssystem für die Steigung a und den
Achsenabschnitt b und kann gelöst werden. Näheres in Press et al: Numerical Recipies.
Übrigens: Dies ist eine (bei normalverteilten Fehlern in 
r) eine ML-Schätzung, die hier aber ausreichend robust ist (was nicht heißt,
dass das nicht besser ginge).
Ergebnis der linearen Regression:
